Базис. Базисное решение

Запишем каноническую ЗЛП (5.3) в развернутом виде:

max (c₁x₁ + c₂x₂ + … +c_nx_n) (5.4)

при ограничениях

a₁₁x₁ + a₁₂x₂ +… +a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ +… +a_2nx_n = b₂ (5.5)

……………………………...

a_m1x₁ + a_m2x₂ +… +a_mnx_n = b_m

х₁≥ 0, х₂≥ 0 …x_n≥ 0

В матрично-векторном виде каноническая ЗЛП (4) будет иметь вид:

max {cx |Ax =b, x≥ 0} (5.6)

где с – вектор коэффициентов целевой функции; х – вектор оптимизируемых переменных;

b - вектор-столбец свободных членов; А – матрица ограничений размером (m x n):

=(A₁,A₂,…,А_j,…,An),

где А_j = 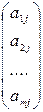- вектор-столбец матрицы А (или вектор ограничений),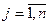

Ограничения (6) в векторной форме можно записать как

A₁х₁ + A₂х₂ +…+ A_nх_n = b (5.7)

Определение8. Вектор х=(х₁,х₂, …,х_n), удовлетворяющий всем ограничениям и условию неотрицательности ЗЛП (5.4), называется допустимым решением (планом) этой задачи.

Определение9. Пусть A₁,A₂,…,A_m (m<n) – множество линейно-независимых векторов ограничений, каждому из которых в ограничениях (5.7) отвечает положительная переменная х_i, допустимого решения. Система m линейно-независимых векторов ограничений А_i, 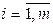, каждому из которых отвечает положительная переменная допустимого решения, называется базисом.

Определение10. Положительные переменные х _i ≥ 0, допустимого решения, каждому из которых отвечает линейно-независимый вектор ограничений А_i, 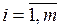, называются базисными переменными, а остальные n-m нулевые переменные – небазисные, то есть

х₁ ≥ 0, х₂ ≥ 0 …x_m ≥ 0 - базисные переменные;

х_m+1= 0, х_m+2 = 0 …x_n =0 - небазисные переменные.

Определение11. Базисное решение х^*, при котором целевая функция принимает максимальное (минимальное) значение, называется оптимальным, то есть f(x) ≤ f(х^*).

¨ Если число базисных переменных равно числу ограничений m, то базисное решение называют невырожденным, а если меньше m, – то вырожденным.

¨ Допустимое множество решений канонической ЗЛП геометрически представляет собой вершины выпуклого многогранника решений.

¨ ЗЛП с невырожденным планом имеет единственное решение (единственную вершину, в которой значение целевой функции оптимально), а ЗЛП с вырожденным планом имеет бесчисленное множество решений (ребро многогранника решений).

Пример3. Найти базисное решение для ЗЛП

f(x)=2x₁ – x₂– x₃ - x₄→ max

при ограничениях

x₁ – x₂ + x₃ =1

2x₁ +x₂ + x₄ =3

х_j ≥ 0,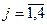

Решение:

1.Запишем матрицу ограничений А:

А₁ А₂ А₃ А₄ А₃ А₄

А=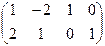 Е =

2. Определим систему линейно-независимых векторов, которые образуют единичную матрицу.

Определение12. Единичной матрицей Е размера (m x m) называют квадратную матрицу, в которой все диагональные элементы а_ii =1, а недиагональные а_ij =0, i≠j.

Так как векторы А₃ А₄ образуют единичную матрицу, то они являются линейно-независимыми. Им отвечают базисные переменные x₃ и x₄, тогда как небазисными будут x₁ =0 и x₂= 0.

3. Из ограничений определим значение базисных переменных x₃ =1 и x₄ =3. Допустимое базисное решение будет

х = (0,0,1,3).

небазисные базисные

Дата добавления: 2014-01-07