Зависимость положения уровня Ферми от температуры для невырожденного полупроводника с частично компенсированной примесью

Рассмотренные случаи чисто донорного и чисто акцепторного полупроводника обычно не реализуются на практике. Как бы тщательно ни проводилась очистка материала, в нем обычно остаются примеси нескольких видов, причем некоторые из примесных центров могут отдавать или присоединять к себе более одного электрона. Остановимся более подробно на случае, когда наряду с донорной примесью в полупроводнике имеется некоторое количество акцепторной примеси (см. рис. 2.13).

Предположим, что в полупроводнике имеется в равных количе­ствах донорная и акцепторная примеси, т. е. N_d=N_a. При тем­пературе абсолютного нуля электроны занимают наиболее низкие энергетические состояния. Это означает, что в зоне проводимости нет электронов, а в валентной зоне – все состояния заняты. Поскольку есть свободные состояния на акцепторной примеси, которые энерге­тически расположены ниже, чем состояния донорной примеси, то электроны, стремясь заполнить состояния с наименьшей энергией, перейдут с донорных уровней на акцепторные. В результате обра­зуются положительные и отрицательные ионы в равных количествах. Условие электронейтральности выполняется, поскольку N_d⁺=N_a^-. Такой полупроводник называют компенсированным. В нем имеет место взаимная компенсация примесей, вследствие чего последние не могут являться поставщиками электронов и дырок, носители заряда возникают в результате тепловой генерации "зона — зона".

В компенсированном полупроводнике из-за наличия примесей периодичность поля решетки нарушена значительно сильнее, чем в истинно собственном. Это будет сказываться на эффектах, связан­ных с рассеянием носителей заряда, в частности на их подвижности.

Предположим, что N_d>N_a и во всей рассматриваемой области температур уровень Ферми лежит значительно выше уровня энергии акцепторной примеси E_a. При этом условии все акцепторные состояния заполнены электронами, пере­шедшими с уровней донорной примеси. В результате, общее количество электронов на донорных уровнях и в зоне проводимости составляет N_d -N_a. Пока не наступит собственная проводимость, свободные дырки в валентной зоне отсутствуют и полупроводник ведет себя как чисто донорный. Такой полупроводник называют частично компенсированным. Степень компенсации определяется отношением N_a/N_d. В таком полупроводнике перенос заряда осуществляется только электронами, и постоянная Холла имеет отрицательный знак.

В случае, когда N_a>N_d и уровень Ферми проходит значительно ниже E_d, донорная примесь полностью ионизована. Все электроны с донорных уровней перешли на уровни акцепторной примеси, поэтому при Т = 0 на атомах акцепторной примеси будет N_a -N_d дырок. С ростом температуры электроны из валентной зоны будут переходить к атомам акцепторной примеси, полупроводник будет вести себя как дырочный, имеющий положительный коэффициент Холла. С наступлением собственной проводимости знак постоянной Холла изменится, так как подвижность электронов больше подвиж­ности дырок.

Определим зависимость концентрации свободных электронов и положения уровня Ферми от температуры в полупроводнике с ча­стично компенсированной примесью для случая N_d>N_a. Условие электронейтральности, при условии, что происходит ионизация только примесных атомов (собственные атомы не ионизуются) имеет вид:

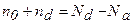или 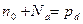(2.94)

Будем считать,что полупроводник невырожден. Используя соотношение

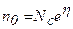
получаем из (2.94) и (2.43):

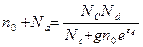(2.95)

Решив это квадратичное уравнение, найдем:

(2.96)

Из соотношения 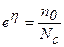определим энергию Ферми

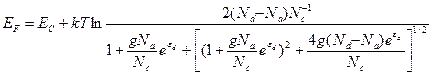(2.97)

Нетрудно видеть, что при N_a =0 найденные выражения совпа­дают с формулами (2.84) и (2.85) для невырожденного донорного полупроводника.

Проведем анализ зависимостей (2.96) и (2.97) для различных температурных условий, а также для различных степеней компенсации.

A. Область НИЗКИХ температур. В области низких температур вид выражений для n₀ и E_F зависит от соотношения концентраций доноров и акцепторов.

(1) Если степень компенсации мала, т. е. N_a<<N_d, то можно найти область температур, для которой выполняется соотношение N_a<<n₀ <<N_d, что эквивалентно условию

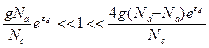(2.98)

В этой области температурные зависимости концентрации и уровня Ферми на основании (2.96) и (2.97) приближенно описы­ваются формулами:

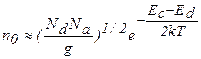(2.99)

(2.100)

совпадающими с выражениями (2.88) и (2.87) для донорного полупроводника. Понятно, что при N_d >> N_а концентрация свободных электронов не зависит от количества акцепторных атомов, как и следует из равенства (2.99). При Т = 0 уровень Ферми лежит в середине между E_c и Е_d. С ростом температуры он понижается (кривая 1 на рис. 2.16 а).

Однако при более низких температурах, когда n₀ << N_a, влиянием акцепторов уже нельзя пренебречь. Положение уровняФермив этой области существенно отличается от того, что имеет место в чисто донорном полупроводнике (соотношение (2.85)).

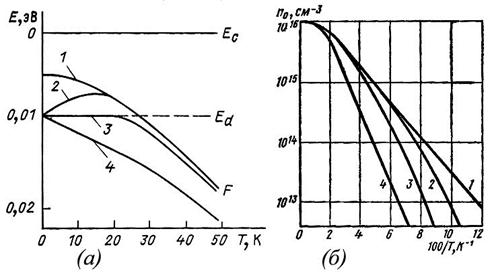
Рис. 2.16. Зависимость положения уровня Ферми (а) и концентрации электронов (б) от температуры в донорном полупроводнике при различной степени компенсации.

Для всех кривых – N_d - N_a = 10¹⁶ cм^-3; N_a равно: 1 – 0; 2 – 10¹⁴; 3 – 10¹⁵; 4 – 10¹⁶ см^-3.

(2) В случае сильной компенсации справедливо неравенство n₀ <<N_a< N_d, поэтому: 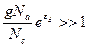и 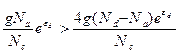(2.101)

и из выражений (2.96) и (2.97) следует:

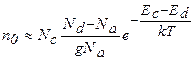(2.102)

(так как g =2) (2.103)

В этом случае энергия активации равна энергии ионизации донорной примеси w = E_c-E_d, т. е. в 2 раза больше, чем у чисто донорного полупроводника.

На основании соотношения (2.103) на рис. 2.16 а построена зависимость E_F(Т), а на рис. 2.16, б изображена зависимость n₀(Т) для различной степени компенсации. На рис. 2.16 а видно, что при повышении температуры, начиная от абсолютного нуля, если:

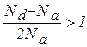
	кривая 2	уровень Ферми вначале повышается от уровня донорной примеси, а затем понижается. В этом случае с увеличением Т растет n0 и неравенство (2.101) перестает выполняться. Как следствие, начинает работать соотношение (2.100) или (2.87) à кривая 2 имеет максимум.
	кривая 3	он остается неизменным, пока выполняется условие по << Na, а затем понижается
	кривая 4	с ростом температуры уровень Ферми снижается от донорного уровня

Из сравнения кривых, представленных на рис. 2.16 б, следует, что температура, при которой наступает насыщение зави­симости n₀(Т), растет с увеличением степени компенсации донорной примеси.

Кривая 1 соответствует отсутствию компенсации: ее поведение соответствует выражению (2.88). Кривая 2 соответствует малой степени компенсации. На ней проявляются три участка. Первый участок (температура выше 30 К на рис. 2.16 б) соответствует полной ионизации, второй участок (область температур 15 – 30 К на рис. 2.16 б) – область половинного наклона, следует зависимости (2.99), и, наконец, третий участок (на рис. 2.16 б – Т < ~ 15-20К) – область целого наклона, описывается формулой (2.102). Сказанное выше относится к случаю N_a << N_d. При более высокой степени компенсации участок половинного наклона укорачивается (кривая 3), и, наконец, он может вовсе не проявляться (кривая 4). Кривые 2 и 3 указывают на то, что компенсация начинает сказываться лишь при достаточно низких температурах

Б. Область средних температур. В области средних температур, когда донорные атомы полностью ионизованы (n_d à 0, p_d à N_d), справедливы неравенства:

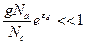и 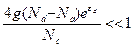(2.104)

Учет этих неравенств дает следующие соотношения:

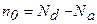(2.105)

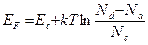(2.106)

Как и следовало ожидать, концентрация свободных электронов постоянна и определяется количеством нескомпенсированной донорной примеси. Уровень Ферми с ростом температуры понижается и при температурах, соответствующих началу собственной проводимости, приближается к середине запрещенной зоны.

В. Область высоких температур. Как и в случае чисто донорного полупроводника, при высоких температурах полупроводник становится собственным, поэтому температурная зависимость E_F имеет вид (2.73), а концентрация – по формулам (2.69) и (2.70).

Дата добавления: 2014-01-07