Динамические и точностные характеристики СВвИ

Конечность времени преобразования t _пр напряжения в двоич­ной код ведет к появлению динамической ошибки , пос­кольку результат преобразования относится практически не к отсчетным моментам времени 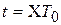(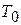- интервал отсчета, 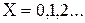), а к случайному моменту времени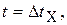 . Можно показать, что математическое ожидание динамической ошибки , а ее дисперсия

,

если распределено в интервале 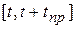равномерно.

Пусть 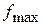- граничная частота спектра сигнала , поступающего на вход АЦП. Тогда в соответствии с теоремой Котельникова

(2.7.9)

где: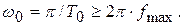

Смещение отсчетной точки относительно момента времени на ве­личину - ведет к появлению динамической ошибки:

(2.7.10)

Полагая

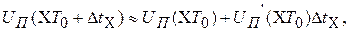
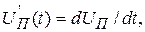найдем

Тогда математическое ожидание ошибки будет равно:

(2.7.11)

Учитывая то, что код на выходе АЦП не должен зависеть от номера отсчета, с учетом выражения (2.7.11) можно написать 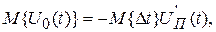так как спектр сигнала так же ограничен частотой 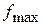(дифференцирование - линейная операция). Выбирая отсчетные точки так, чтобы , получим .

Положим, что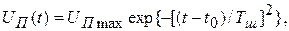

где: 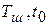- некоторые константы. Тогда максимальное значение

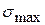где: е - основание натурального логарифма, а Откуда видим, что увеличивается с уменьшением , а это означает, что на мелких деталях контрастная чувствительность зрения понижается.

Функция порогового контраста ,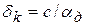

где: 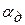- угол зрения, под которым рассматривается деталь изображения, а с=6.28.10^-5, при . Найдем максималь­ное значение =, при котором динамическая ошибка преобразования не будет замечена человеком на выведеном изображении, из условия , полагая, что во всем интервале яркостей элементов этого изображения справедлив закон Вебера-Фехнера и шум квантования незаметен. Поскольку:

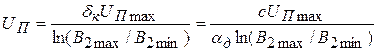(2.7.12)

имеем:

(2.7.13)

Пycть временные размеры наблюдаемой детали изображения составляют (сигнал отсчитывается по уровню, равному 0,02 ), наблюдение ведется с расстояния . Тогда .

где: 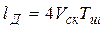- линейные размеры детали изображения; - скорость скани­рования. С учетом последних соотношений найдем максимальное вре­мя преобразования:

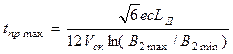(2.7.14)

Для значений 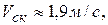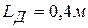, получим .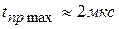

Точностные характеристики СВвИ зависят, как правило, от точ­ности и стабильности работы его электронных и электромеханических компонент, номенклатура которых между собой опреде­ляется принципом работы устройства.

Пусть - координаты соответствующих точек на исходном изображении и на выходном (репродукции), представленных на стандартных листах в системах координат, связанных с их краями, а - машинные значения этих координат, 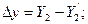- погрешности ввода-вывода, которые зависят от принципа развертки. Широкое распространение получили СВвИ с электро­механической разверткой барабанного типа, где стабильность шагов дис­кретизации снимка по строкам и по кадру 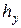связана с точностью изготовления электромеханических средств развертки. Если электроме­ханические узлы выполнены с приемлемыми (с точки зрения качества) погрешностями (на биения, люфты, вибрации и т.п.), то ими можно пренебречь. Тогда . 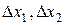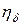Значения в аналогичных условиях зависят от стабильности по , где- радиус барабана, - угловая скорость вращения барабана, - частота строчной дискретизации изображения. Находя полный дифференциал этого выражения и заменяя все дифференциалы конечными приращениями, получим:

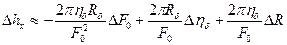(2.7.15)

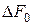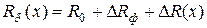Расчеты показывают, что при мм составляющими связанными с и можно пренебречь, если нес­табильность строчной частоты синхронизации и вращения барабана не превышает . Как правило это имеет место, поскольку частота синхронизации стабилизированы кварцевым и камертонным элементами соответственно. Тогда, полагая , а радиус барабана , най­дем для элемента с координатой X:

(2.7.16)

где: - систематичес­кая погрешность, связанная, например, с использованием фотоматериа­ла на бумаге нестандартной толщины, 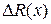- погрешность, вызванная некачественной обработкой поверхности барабана. Как правило составляющей можно пренебречь. Что же касается первой составляющей, то уже при , она может достигнуть в конце строки 0,3 мм. Стабиль­ность шагов и 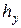связана с идентичными рассмотренным факторами, таки­ми как точность изготовления механических узлов и погрешности электромеханического проецирования изображения. Заметим, что нелинейные искаже­ния растра ЭЛТ могут быть достаточно скомпенсированы аппаратурными или прог­раммными средствами до 0,5 элемента разложения. При 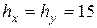мкм механические детали должны изготовляться с точностью 5 мкм. Тогда погрешности электромеханического проецирования могут достигать значения 10мкм.

Представленные качественные и количественные оценки характеристик устройств ввода положены в основу разработки построения контроллеров устройств ввода графической информации, налагаемой на картографический фон интерактивных геоинформационных комплексов оперативного взаимодействия.

Дата добавления: 2014-01-07