Линейного программирования

Понятие двойственности для симметричных задач

Двойственность в линейном программировании

(ПР № 7)

Каждой задаче ЛП, которую назовём исходной (прямой), можно поставить в со­ответствие некоторую другую задачу ЛП, называемую двойственной (обратной).

Двойственная задача – это задача, получаемая с помощью определённых правил непосредственно из условий исходной.

Пример 1. Прямая задача: составление дневного рациона для животных.

Витамин	Корм	Суточная потребность
E
F
PP

Пусть на данном этапе наиболее важными являются три питательных вещества - витамины E, F и PP. В распоряжении фермера имеется два вида дополнительного корма, в которых со­держатся эти витамины. Содержание витаминов в единице кормов и суточная потреб­ность в витаминах приведены в таблице.

Стоимость единицы каждого корма равна, соответственно, 13 и 8 денежных единиц.

Требуется составить дневной рацион, удовлетворяющий данной питательности и имеющий минимальную стоимость.

Математическая модель задачи

Переменные: - количество первого корма, - количество второго корма, включае­мых в ежедневный рацион.

Ограничения на переменные. Дневной рацион будет удовлетворять требуемой пита­тельности, если количество витаминов не меньше предусмотренного:

.

Целевая функция. Цель данной задачи – добиться минимальных затрат на дневной рацион, общую стоимость рациона можно выразить в виде линейной функции

.

Обратная задача: назначение цен на витамины.

Предположим, что все требуемые витамины можно приобрести раздельно у некото­рой фирмы. Эта фирма, назначая цены на витамины, стремится максимизиро­вать свой доход. Но её товар должен быть конкурентоспособен с наборами витаминов, содержащихся в различных кормах.

Математическая модель задачи

Переменные: - цена витамина E, - цена витамина F, 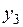- цена витамина PP.

Целевая функция. Продавая суточный набор витаминов по ценам , фирма полу­чит доход .

Ограничения на переменные. Используя единицу 1-го корма, фермер затрачивает 13 денежных единиц, получая определённый набор витаминов.

У фирмы этот же набор витаминов будет стоить 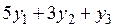(ден.ед.). Поэтому назначая цены на витамины, фирма должна следить за выполнением условия

.

Аналогично, для 2-го корма:

.

Получаем следующую систему неравенств:

.

Пример 2. Прямая задача: составление плана производства предприятия.

Вид сырья	Количе-ство сырья	Количество единиц сырья, идущих на изготовление единицы продукции
Р1	Р2	Р3
S1
S2
Цена одного изделия (ден.ед.)

Из отходов основного производства предприятие может наладить выпуск трёх видов продукции Р₁, Р₂ и Р₃. Количество отходов (сырья), расход сырья на изготовление одного изделия каждого вида, а также цена одного изделия приведены в таблице.

Требуется составить такой план выпуска неосновной продукции, при котором доход от её реализации будет максимальным.

Математическая модель задачи

Переменные: - количество продукции Р₁, - количество продукции Р₂, 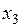- количество продукции Р₃, запланированные к производству.

Ограничения на переменные. Для изготовления продукции потребуется (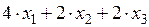) единиц сырья S₁ и () единиц сырья S₂. Так как потребление ресурсов S₁ и S₂ не должно превышать их запасов (35 и 48 единиц соответственно), то связь между потреблением ресурсов и их запасами выразится системой неравенств:

Целевая функция. Суммарный доход составит ден.ед. от реализации продукции Р₁, 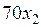ден.ед. - от реализации продукции Р₂, и ден.ед. - от реализации продукции Р₃, т.е.

.

Обратная задача: назначение цен на сырьё.

Предположим, что предприятие при изучении вопроса об использовании отходов основного производства рассматривает возможность их продажи. Требуется назначить такие цены на сырьё, при которых суммарная стоимость сырья была бы минимальной (чтобы заинтересовать покупателей), но чтобы выручка от продажи была не меньше той, что могло бы получить предприятие, организовав собственное производство.

Математическая модель задачи

Переменные: - цена единицы сырья S₁, 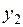- цена единицы сырья S₂.

Целевая функция. Продавая отходы основного производства по ценам и 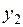, пред­приятие полу­чит доход

.

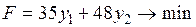Ограничения на переменные.

Для удовлетворения требований продавца сумма, вырученная от продажи сырья (идущего на изготовление единицы продукции), должна быть не меньше цены соответствующей продукции.

Получаем следующую систему неравенств:

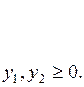
Сопоставляя модели прямой и обратной задач, можно установить следующие взаимосвязи.

1. Каждому ограничению прямой задачи (ПЗ) соответствует переменная обрат­ной задачи (ОЗ).

2. Каждой переменной прямой задачи соответствует ограничение обратной за­дачи.

3. Коэффициенты при некоторой переменной в ограничениях прямой задачи ста­новятся коэффициентами левой части соответствующего ограничения обратной задачи (матрица А коэффициентов при переменных в ограничениях ПЗ в обратной задаче транспонируется ), а коэффициент при той же переменной в целевой функции ПЗ становится свободным членом этого же ограничения ОЗ.

4. Правые части ограничений ПЗ становятся коэффициентами при переменных в целевой функции ОЗ.

5. Если прямая задача на максимум, а система ограничений представляется в виде неравенств типа ≤, то обратная задача решается на минимум, а её система огра­ничений имеет вид неравенств типа ≥, и наоборот.

Пары взаимно двойственных симметричных задач в виде конечных сумм имеют вид:

прямая задача		двойственная задача
,		,
;		;

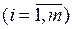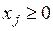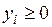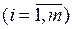прямая задача		двойственная задача
,		,
;		.

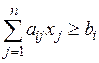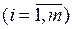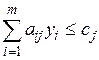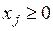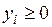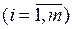Пример 1. Составить задачу, двойственную следующей задаче:

.

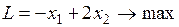
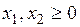Р е ш е н и е. Так как исходная задача на максимизацию, то приведём все нера­венства системы ограничений к виду ” ≤ ”, для чего обе части 1-го и 4-го неравенств умножим на -1. Получим

Сформулируем двойственную задачу:

.

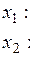
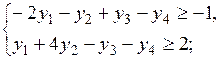
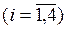Дата добавления: 2014-01-07