Касательные напряжения при изгибе

ЛЕКЦИЯ №12

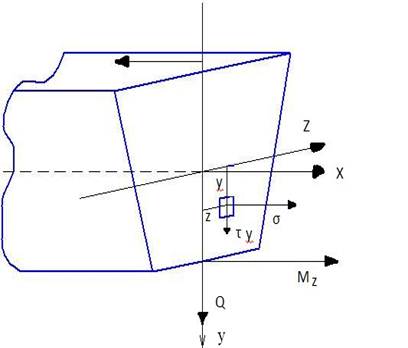При поперечном изгибе в поперечных сечениях балки действуют не только изгибающие моменты, но и поперечные силы. Изгибающие моменты вызывают в поперечных сечениях бруса нормальные напряжения, а поперечные силы – касательные напряжения.

Имеем следующие интегральные зависимости

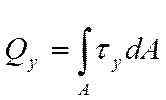
Получим формулу касательных напряжений при изгибе. Вывод формулы основывается на двух допущениях:

1) Касательные напряжения принимаются параллельными поперечной силе;

2) Касательные напряжения по ширине сечения на данном уровне одинаковы, а по высоте сечения меняются.

Выделим из балки элемент двумя параллельными и одним продольным сечениями dx.

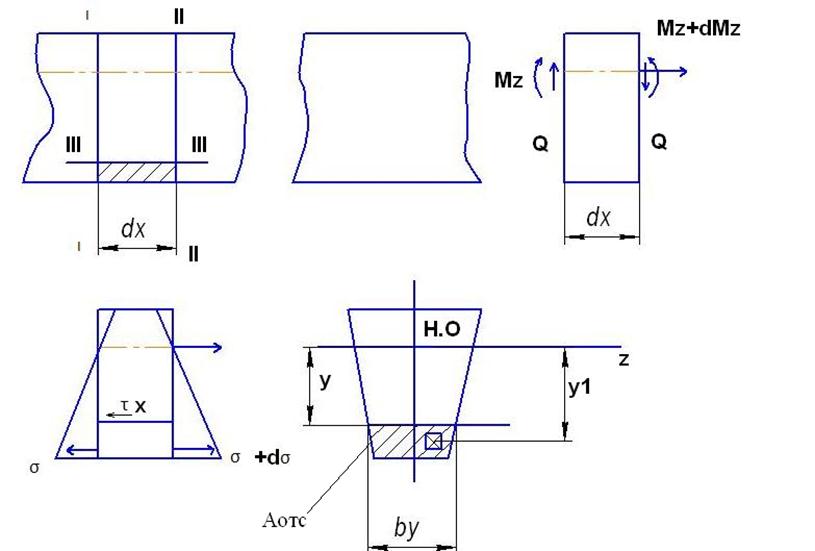
N₁ – равнодействующая нормальных σ на А_отс в сечении I – I

N₂ – равнодействующая нормальных в сечении I I – I I

Т – равнодействующая касательных напряжений в сечении III – III

Спроектируем все силы на ось X

(*)

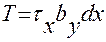
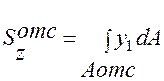- статистический момент площади отсеченной части сечения, относительно нейтральной оси Z.

По закону парности кас. напряжений τ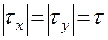

Полученные выражения для N_1, N_2, Т подставим в (*).

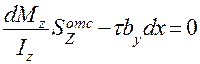:dx учтем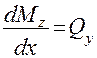

формула касательных напряжений при изгибе. Формула Журавского.

Для определения τ в данной точке сечения необходимо:

1. Определить поперечную силу в данном сечении

2. Определить ширину сечения b_y по линии обреза m-m проходящей через данную точку

3. Определить статический момент площади части сечения расположенной выше (или ниже)линии обреза m-m, относительно нейтральной оси (S_z =0, то сумма для верхней и нижней частей дает ноль)

4. Определить осевой момент инерции сечения относительно нейтральной оси Z

Подставляя полученные значения величин в формулу Журавского, найдем касательные напряжения в данной точке.

Знак касательных напряжений определяется знаком поперечной силы.

Распределение касательных напряжений при изгибе для некоторых форм сечений

1. Прямоугольное сечение

Примем Q>0, следовательно, τ>0.

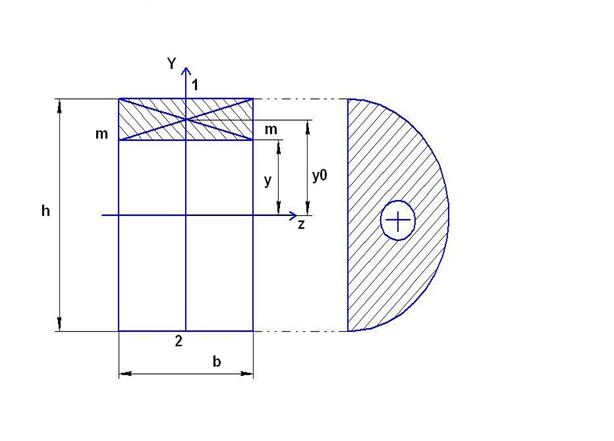
Определяем касательные напряжения в точках на расстоянии y от нейтральной оси Z

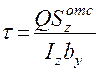
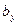=b, A=bh.

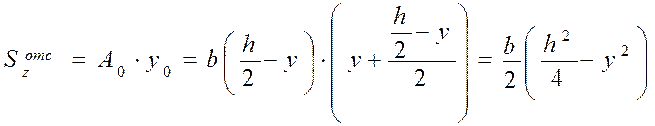
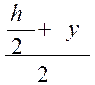
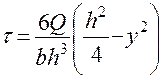
Касательная напряжения по высоте сечения изменяются по закону квадратной параболы.

Чтобы построить эпюру «τ» надо знать напряжения в трех точках:

Точки 1,2 при y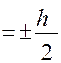 τ_1,2=0

при y=0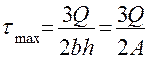

2.Треугольное сечение

Формула Журавского дает приближенный характер напряжений, но применяется

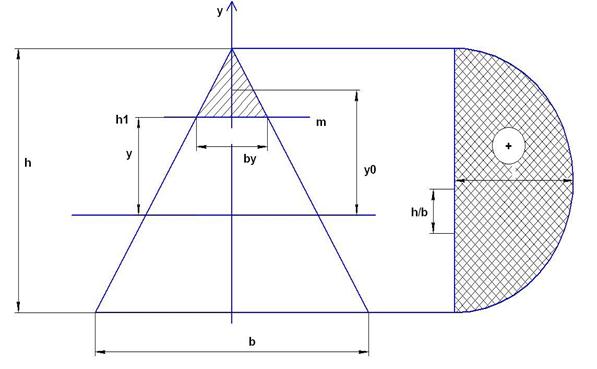
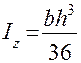
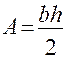
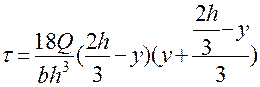
При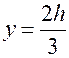

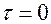
При

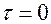
- не на нейтральной оси, а при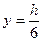

.

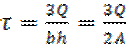
3.Круглое сечение

Квадратная парабола

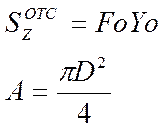
4.Двутавровое сечение

,

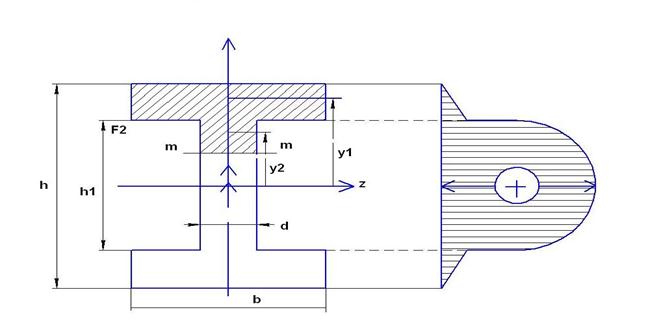
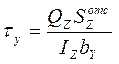Целесообразно разбить отсеченную часть на простые фигуры.

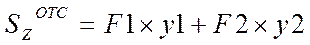- это в общем виде.

Таким образом, можно найти τ в пределах высоты стенки. Поперечная сила Q>0 и следовательно τy>0. Они действуют вертикально.

Формула Журавского для веритикальных касательных напряжений в полках дает результаты отличные от действительных (т.е. формулой пользоваться нельзя).

В действительности вертикальные касательные напряжения в полках весьма малы и ими можно пренебречь.

В полках двутавра кроме вертикальных напряжений τ действуют горизонтальные напряжения τ.

Горизонтальные касательные напряжения могут быть получены, используя так же формулу Журавского.

Поток касательных напряжений идет как вода в русле. И поэтому в полках действует касательные напряжения.

Проведем на левой верхней полке линию обреза и отсчет площадь Fn (полки)

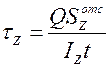
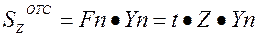
Условия прочности при изгибе по касательным напряжениям

Наибольшие τ в балке не должны превышать допускаемых τ для материала

.

По эпюре «Q» выбираем Qmax. В том сечении где действует Qmax выбираем точки в которых действуют максимальные τ.

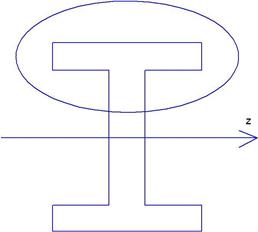Для двутавра берем by=d и Qmax - поперечная сила в опасном сечении берется по модулю.

Подбор размеров сечения делается из условия прочности по σ, а затем делают проверку по τ, но часто ее не делают.

Проверка прочности по τ производится в обязательном порядке в следующих случаях

1. Для коротких металлических балок (L – мало, и Мизг мал, а τможет быть больше)

2. Для длинных металических балок, если вблизи опор имеются сосредотачиваются силы большой величины. (Мизг мал, а Q велика и может балку перерезать около опоры)

3. Для деревянных балок, т.к. дерево плохо работает на скалывание

Дата добавления: 2014-01-07