
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аксиомы (схемы аксиом) исчисления высказываний
|
|
|
|
Лекция 5
Исчисление = формальная аксиоматическая теория.
Язык (алфавит, формулы), аксиомы, правила вывода.
(A1) 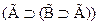 ;
;
(A2) 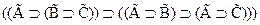 ;
;
(A3) 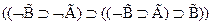 .
.
Правило вывода: из 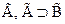 непосредственно следует
непосредственно следует 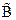
Теорема дедукции:
- Если Г - множество формул,
 и
и 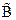 - формулы и
- формулы и 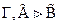 , то
, то 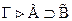 .
. - В частности, если
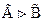 , то
, то 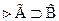 .
.
Утверждение доказано по индукции.
Замечания:
1. При доказательстве использованы только схемы аксиом (А1) и (А2).
2. Доказательство позволяет по выводу 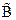 из Г и
из Г и  построить вывод
построить вывод 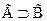 из Г.
из Г.
Следствия:
1. 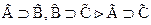 . Действительно, ведь из
. Действительно, ведь из 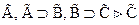 .
.
2. 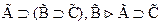 . Действительно, ведь из
. Действительно, ведь из 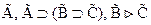 .
.
3. 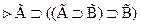 . Действительно, ведь
. Действительно, ведь 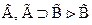
Доказательство нескольких утверждений (a - g)
(a). 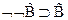
(b). 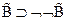
(c). 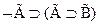
(d). 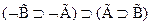
(e). 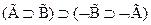
(f). 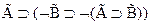
(g). 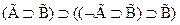
Нам понадобятся (b),(c),(f),(g) и аксиома А1.
Утверждение: Формула теории L является теоремой теории L, тогда и только тогда, когда она является тавтологией.
Þ Утверждение: Всякая теорема теории L является тавтологией.
Ü Теорема о полноте теории L: Если формула теории L является тавтологией, то она является теоремой теории L.
Пусть  - формула, а
- формула, а 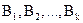 -пропозициональные буквы, входящие в
-пропозициональные буквы, входящие в  .
.
Пусть задано некоторое распределение истинностных значений для 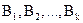 .
.
Обозначим: 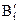 есть
есть 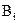 , если
, если 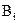 принимает значение «истина» и
принимает значение «истина» и 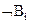 , если
, если 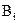 принимает значение «ложь».
принимает значение «ложь».
Обозначим’: 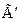 есть
есть  , если при заданном распределении истинностных значений
, если при заданном распределении истинностных значений  принимает значение «истина», и
принимает значение «истина», и 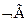 , если
, если  принимает значение «ложь».
принимает значение «ложь».
Лемма. 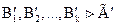 . (Лемма о выводимости из литералов)
. (Лемма о выводимости из литералов)
Например для формулы 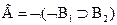 при
при 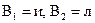
 принимает значение «ложь», поэтому, лемма утверждает, что
принимает значение «ложь», поэтому, лемма утверждает, что 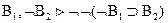
Доказательство леммы: Индукция по числу n вхождений в  пропозициональных связок.
пропозициональных связок.
n=0, то  - пропозициональная буква
- пропозициональная буква 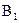 , утверждение леммы сводится к
, утверждение леммы сводится к 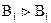 и
и 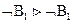 .
.
Допустим, что лемма верна при любом j<n. Пусть 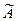 имеет ровно n связок.
имеет ровно n связок.
| Связка | Формула 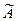
| Значения 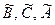
| Случай |
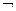
| 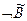
| И, -, Л | 1а |
| Л, -, И | 1б | ||
| Л, -, И | 2а | ||
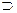
| 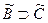
| -, И, И | 2б |
| И, Л, Л | 2в |
Случай 1а: 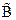 =И,
=И,  =Л. Тогда
=Л. Тогда 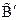 =
=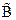 , а
, а 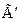 =
=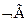 =
=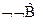 .
.
По индуктивному предположению, примененному к 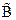 ,
, 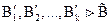 ,
,
1. 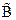
2. 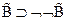 (b)
(b)
3. 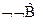 по МП 1. и 2.
по МП 1. и 2.
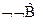 есть
есть 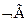 или
или 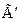 . Следовательно
. Следовательно 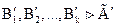
Случай 1б: 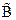 =Л,
=Л,  =И. Тогда
=И. Тогда 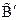 =
=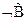 , а
, а 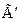 =
= =
=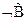 .
.
По индуктивному предположению, примененному к 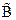 ,
, 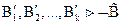 .
.
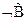 есть
есть  или
или 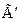 . Следовательно
. Следовательно 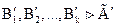
Случай 2а: 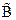 =Л,
=Л,  =И, Тогда
=И, Тогда 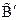 =
=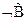 ,
, 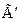 =
= =
= 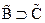 .
.
По индуктивному предположению 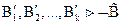 .
.
1. 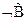
2. 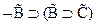 (с)
(с)
3. 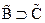 МП
МП
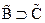 есть
есть  или
или 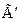 . Следовательно
. Следовательно 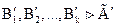
Случай 2б: 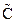 =И,
=И,  =И. Тогда
=И. Тогда 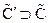 ,
, 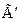 =
= =
= 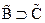
По индуктивному предположению 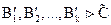 .
.
1. 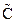
2. 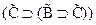 (А1)
(А1)
3. 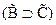 МП
МП
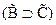 есть
есть  , или
, или 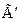 . Следовательно
. Следовательно 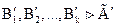
Случай 2в: 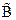 =И,
=И, 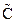 =Л,
=Л,  =Л. Тогда
=Л. Тогда 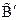 =
=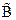 ,
, 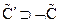 ,
, 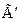 =
=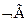 =
= 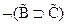 .
.
По индуктивному предположению 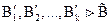 , и
, и 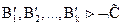 .
.
1. 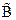
2. 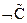
3. 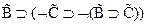 (f)
(f)
4. 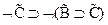
5. 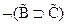
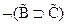 , есть
, есть или
или 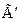 . Следовательно
. Следовательно 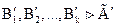
Лемма доказана.
Доказательство теоремы о полноте:
Пусть  - тавтология, а
- тавтология, а 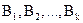 - пропозициональные буквы, входящие в
- пропозициональные буквы, входящие в  .
.
Для любого распределения истинностных значений 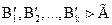 (тавтология!)
(тавтология!)
В частности, 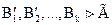 и
и 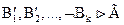 .
.
По теореме дедукции 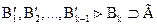 и
и 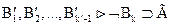
По (g) и дважды МП 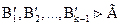 .
.
Так последовательно исключая все 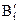 , получим
, получим 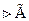 . Теорема о полноте доказана.
. Теорема о полноте доказана.
Следствие:
Теория L - непротиворечива.
Доказательство: Поскольку всякая теорема теории является тавтологией, отрицание тавтологии – невыводимо.
Доказательство утверждений (a - g)
(a). 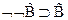
1 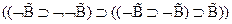 - (A3(
- (A3(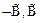 ))
))
2 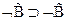 - теорема (1)
- теорема (1)
3 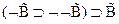 - 1,2 по следствию 2
- 1,2 по следствию 2
4 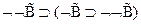 - (А1(
- (А1(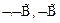 ))
))
5 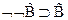 - 3,4 по следствию 1
- 3,4 по следствию 1
(b). 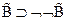
1. 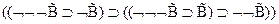 - (А3(
- (А3(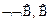 ))
))
2. 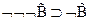 - пункт (а)
- пункт (а)
3. 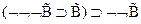 - 1,2 по МП
- 1,2 по МП
4. 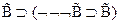 - (А1(
- (А1(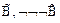 ))
))
5. 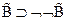 - 3,4 по следствию 1
- 3,4 по следствию 1
(c). 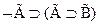
По теореме дедукции достаточно доказать, что 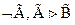
1. 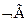 - гипотеза
- гипотеза
2.  - гипотеза
- гипотеза
3. 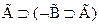 - (А1)
- (А1)
4. 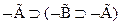 - (А1)
- (А1)
5. 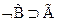 - 2,3 по МП
- 2,3 по МП
6. 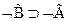 - 1,4 по МП
- 1,4 по МП
7. 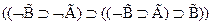 - (А3)
- (А3)
8. 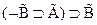 - 6,7 по МП
- 6,7 по МП
9. 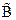 - 5,8 по МП
- 5,8 по МП
(d). 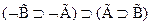
По теореме дедукции достаточно доказать, что 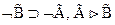
1 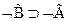 - гипотеза
- гипотеза
2  - гипотеза
- гипотеза
3 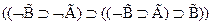 - (А3)
- (А3)
4 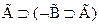 - (А1)
- (А1)
5 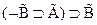 - 1,3 по МП
- 1,3 по МП
6 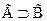 - 4,5 по следствию 1
- 4,5 по следствию 1
7 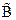 - 2,6 по МП
- 2,6 по МП
(e). 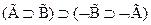
По теореме дедукции достаточно доказать, что 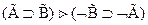
1 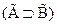 - гипотеза
- гипотеза
2 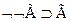 - пункт (а)
- пункт (а)
3 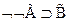 - 1,2 по следствию 1
- 1,2 по следствию 1
4 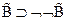 - пункт (в)
- пункт (в)
5 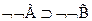 3,4 по следствию 1
3,4 по следствию 1
6 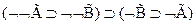
7 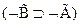 - 5,6 по МП
- 5,6 по МП
(f). 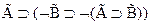
1 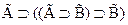 - следствие 3
- следствие 3
2 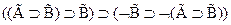 - пункт (е)
- пункт (е)
3 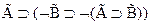 - 1,2 по следствию 1
- 1,2 по следствию 1
(g). 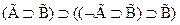
По теореме дедукции достаточно доказать, что 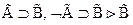
1 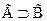 - гипотеза
- гипотеза
2 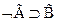 - гипотеза
- гипотеза
3 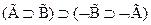 - пункт (е)
- пункт (е)
4 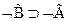 1,3 по МП
1,3 по МП
5 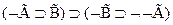 - пункт (е)
- пункт (е)
6 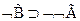 - 2,5 по МП
- 2,5 по МП
7 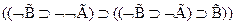 - (А3)
- (А3)
8 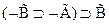 - 6,7 по МП
- 6,7 по МП
9 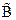 - 4,8 по МП
- 4,8 по МП
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1984; Нарушение авторских прав?; Мы поможем в написании вашей работы!