Решение уравнений переменных состояния в частотной области

Применим к уравнению прямое преобразование Лапласа:

,

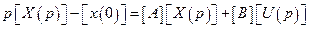где 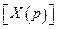и 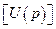- преобразования по Лапласу вектора переменных состояния и вектора входных воздействий соответственно. Тогда, решая это уравнение относительно 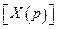, получим:

,

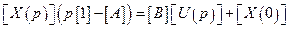
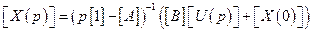тогда изображение по Лапласу для выходного вектора выглядит следующим образом:

,

.

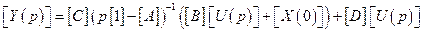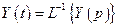Главное достоинство этого подхода состоит в том, что в результате мы получаем аналитическое решение.

Возьмем теперь нулевые начальные условия, 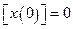, тогда

.

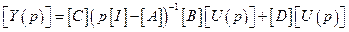Но мы говорили о том, что для 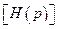существует следующее выражение:

,

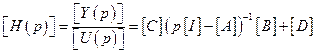где 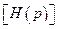- это матричная передаточная функция для системы с 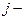входов и 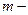выходов. Т.е. решение уравнения переменных состояния в частотной области позволяет в явном виде определить передаточную функцию для системы с 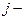входами и 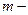выходами, что достаточно важно на практике.

Мы пока будем работать с системой с одним входом и одним выходом. Вернемся к матрице 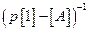, которая по определению равна:

,

где знаменатель – скалярное выражение, полином 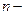й степени, а числитель – сумма матриц, умноженная на оператор Лапласа в соответствующей степени. Существует алгоритм Суриана-Фрейма, позволяющий определить матричные коэффициенты числителя и степени 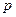, на которые они будут умножаться, а также скалярные коэффициенты знаменателя. Знаменатель 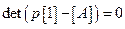представляет собой характеристическое уравнение системы (как раз то, которое мы получали из однородного дифференциального уравнения, из 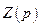для операторного метода). Разложим этот полином на множители:

,

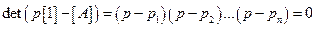где 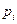- собственные частоты системы.

Теперь можем сформулировать следующие выводы:

1) Как только мы определили собственные частоты системы, с точностью до постоянного множителя становится известным знаменатель передаточной функции.

2) В зависимости от того, будут или не будут сокращаться 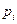с корнями функции числителя, они будут или не будут являться полюсами передаточной функции.

В линейной алгебре 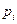называются собственными значениями матрицы . Для их определения используется целый ряд алгоритмов, наиболее эффективным из которых является алгоритм QR.

Как-либо формально обозреть числитель рассматриваемого выражения и дать ему трактовку невозможно, однако поставим задачу определить нули этой функции. Сведем задачу нахождения нулей передаточной функции к определению полюсов некоторой вспомогательной системы. Для простоты будем рассматривать одномерный случай.

Итак, пусть для нашей системы заданы функции входа и выхода и передаточная функция (см. рисунок).

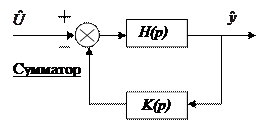Введем понятие систем с обратными связями. Они используются для следующих целей. Когда мы подаем сигнал на основное звено системы 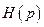, ясно, что у входного сигнала возможны какие-либо отклонения от номинального значения, которые 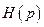передаст и на выход. Чем меньше отклонения от начального значения сигнала, тем лучше. Уменьшить отклонения можно следующим образом. Можно взять звено обратной связи 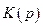, подать выходящий сигнал на это звено, и вывести его на сумматор (см. рисунок). Таким образом нам удастся снизить нестабильность реакции цепи на возмущениях.

Итак, пусть в системе есть основное звено 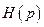, звено обратной связи 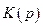, тогда система, состоящая из этих двух звеньев называется системой с обратными связями.

Попробуем «перевернуть» эту систему: возьмем за основу звено обратной связи 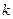(не зависящее от 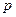), в цепь обратной связи поставим прямое звено 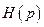(см. рисунок). То, что относится к внешней системе, будем на рисунке снабжать «крышечками». Такая система называется обратной системой. Поскольку наша система обладает одним входом и одним выходом,

,

.

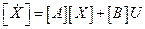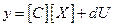Находим передаточную функцию обратной системы:

.

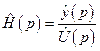Учтем, что 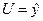, тогда

.

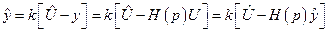Раскрывая скобки, получим:

.

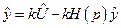
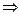
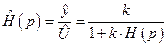Возьмем предел от этого выражения при :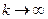

,

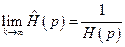значит нули 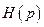будут полюсами 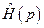, а полюса 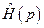- нулями исходной передаточной функции.

Итак, чтобы определить нули исходной передаточной системы, нам нужно проделать следующее:

1. сформировать основную матрицу обратной системы ;
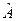2. определить ее полюса (собственные значения) 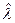с помощью QR алгоритма;
3. взять предел при .

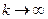Вспоминаем второе уравнение для основной системы:

,

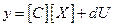тогда

.

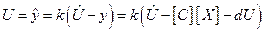
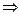
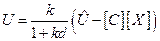Теперь мы можем получить основное уравнение для обратной системы:

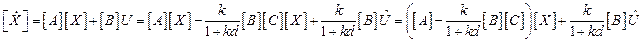
Поскольку 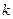не зависит от 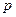, новых реактивных элементов в обратную схему мы не привнесли. А значит при формировании обратной системы вектор переменных состояния 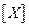исходной и обратной систем совпадают. Значит полученное уравнение действительно является основным уравнением для обратной системы:

.

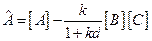[1] Аппроксимация - приближенное выражение некоторых величин или объектов через другие более простые величины или объекты.

Дата добавления: 2014-01-07