Кривые второго порядка

СЛАУ.

Рассмотрим систему линейных алгебраических уравнений (СЛАУ) относительно n неизвестных x₁, x₂,..., x_n:

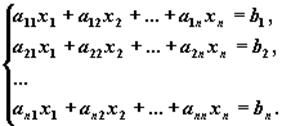
Эта система в "свернутом" виде может быть записана так:

S ⁿ_i=1a_ij x_j = b_i, i=1,2,..., n.

В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричной форме Ax=b, где

, , .

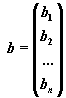Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец x, элементы которой - искомые неизвестные, называется решением системы.

Система линейных алгебраических уравнений, записанная в виде Ax=b, является матричным уравнением.

Если матрица системы невырождена, то у нее существует обратная матрица и тогда решение системы Ax=b дается формулой:

x=A ^-1 b.

Справедливо следующее утверждение (формулы Крамера).

Если определитель D=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x₁, x₂,..., x_n, определяемое формулами Крамера

x_i = D _i / D, i=1,2,..., n,

где D _i - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом правых частей b.

Пример. Вычисление решения системы линейных уравнений по формулам Крамера.

Решить систему:

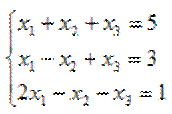
D=|A|=6

х₁ = 12/6=2, х₂ = 6/6=1, х₃ = 12/6=2.

Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x₁, x₂,..., x_n

приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей

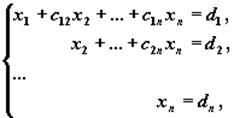
решение которой находят по рекуррентным формулам:

x_n =d_n, x_i = d_i -S ⁿ_k=i+1 c_ik x_k, i=n-1, n-2,...,1.

Матричная запись метода Гаусса.

1. Прямой ход метода Гаусса: приведение расширенной матрицы системы

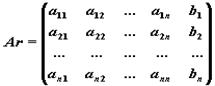
к ступенчатому виду

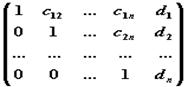
с помощью элементарных операций над строками матрицы (под элементарными операциями понимаются следующие операции:

o перестановка строк;

o умножение строки на число, отличное от нуля;

o сложение строки матрицы с другой строкой, умноженной на отличное от нуля чиcло).

1. Обратный ход метода Гаусса: преобразование полученной ступенчатой матрицы к матрице, в первых n столбцах которой содержится единичная матрица
   ,
   последний, (n+1) -й, столбец этой матрицы содержит решение системы.

Пример.
Решить систему уравнений методом Гаусса.

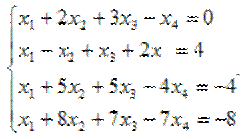
Решение:

Выписав расширенную матрицу этой системы, после ряда элементарных преобразований (проследить порядок которых рекомендуем самостоятельно), получим:

откуда

Решая последнюю систему, находим

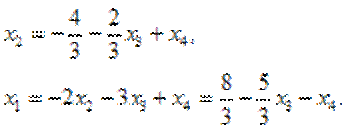
Здесь ранг расширенной матрицы равен рангу основной матрицы и равен, очевидно, двум. Система имеет бесконечно много решений, каждое из которых можно получить, придавая х₃ и х₄ конкретные значения.

Опр.

Это такое геометрическое место точек на плоскости, уравнение которого имеет вид:

(1)

в котором, по крайней мере один из коэффициентов 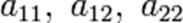отличен от нуля.

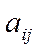- числа коэффициенты

,

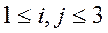
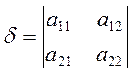Дата добавления: 2014-01-07