
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кинематика
|
|
|
|
При исследовании кинематики планетарных передач широко используют метод остановки водила – метод Виллиса.
Всей планетарной передаче мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. При этом водило как бы затормаживается, а все другие звенья освобождаются. Получаем так называемый обращенный механизм (см.рис.10.1,в), представляющий собой простую передачу, в которой движение передается от a к b через паразитное колесо g. Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила. В качестве примера проанализируем кинематику передачи, изображенной на рис.10.1. Условимся приписывать частотам вращения индекс звена (na, nH и т.д.), а передаточные отношения сопровождать индексами в направлении движения и индексом неподвижного звена. Например,  - означает передаточное отношение от a к Н при неподвижном b. Для обращенного механизма
- означает передаточное отношение от a к Н при неподвижном b. Для обращенного механизма
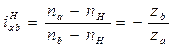 , (10.1)
, (10.1)
так как сателлит является здесь паразитным колесом.
В планетарных передачах существенное значение имеет знак передаточного отношения. Условимся, что при i > 0 – вращение ведущего и ведомого звеньев происходит в одном направлении; при i < 0 – вращение противоположное. В рассматриваемом примере колеса a и b вращаются в разных направлениях, а поэтому  < 0.
< 0.
Переходя к реальному механизму, у которого в большинстве случаев практики колесо b закреплено, a - ведущее и Н – ведомое, на основе формулы (10.1) при nb = 0 получаем:

или
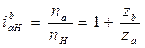 . (10.2)
. (10.2)
Частоту вращения сателлита определим из равенства
 . (10.3)
. (10.3)
При заданных na и nH определяют ng или (ng - nH) как частоту вращения сателлита относительно водила (используют при расчете подшипников).
Далее имеем
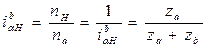 . (10.4)
. (10.4)
Для случая, когда неподвижно колесо a, на основе формулы (10.5) при na = 0 с помощью аналогичных преобразований находим:
 , (10.6)
, (10.6)
 . (10.7)
. (10.7)
Анализ кинематики планетарных передач, выполненных по другим схемам, производят таким же методом.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 313; Нарушение авторских прав?; Мы поможем в написании вашей работы!