Монотонные последовательности

Лекция 10. Свойства последовательностей.

Марциал, Эпиграммы, V, 56.

«Пристаешь ты давно ко мне с вопросом,

Луп, кому обученье сына вверить.

Всех и риторов ты и грамотеев,

Мой совет, избегай: не надо сыну

Знаться ни с Цицероном, ни с Мароном.

Пусть Тутилий своей гордится славой!

Если ж сын стихоплет, – лиши наследства.

Хочет прибыльным он заняться делом?

Кифаредом пусть будет иль флейтистом.

Коль окажется мальчик тупоумен,

Пусть глашатаем будет или зодчим …».

Соответствует ли эта оценка действительности? Какое положение занимал архитектор в Римской империи?

14. Эти две разновидности архитектурных деталей нашли широкое применение в Поздней империи:

(…) (фр.) – ряд арок, опирающихся на столбы или колонны.

(…) (нем.) – архитектурный пояс, архитектурный фриз – украшение стены в виде ряда глухих арочек, часто опирающихся на консоли и кронштейны, иногда – на колонки.

Определение 10.1. Последовательность 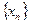называется неубывающей (невозрастающей), если справедливо неравенство 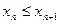() для всех 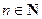. Если неравенства строгие – последовательность называется возрастающей (убывающей).

Определение 10.2. Последовательность 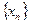называется монотонной, если она является либо неубывающей, либо невозрастающей; строго монотонной – если она является возрастающей или убывающей.

♦ Утверждение 10.1. Невозрастающие (убывающие) последовательности ограничены сверху, неубывающие (возрастающие) – снизу.

♦ Теорема 10.1. Если неубывающая (невозрастающая) последовательность ограничена сверху (снизу), то она сходится.

Доказательство. Рассмотрим случай неубывающей и ограниченной сверху последовательности 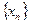. Так как множество всех элементов последовательности ограничено сверху, то существует . По определению следует, что . Таким образом, 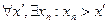или , .

По определению неубывающей последовательност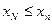и при 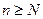, но тогда , то есть , при 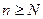. Имеем . Получаем, что 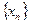сходится и имеет пределом .

Аналогично, доказывается факт, что невозрастающая и ограниченная последовательность сходится к . ■

☼ Замечание 10.1. Условие ограниченности монотонной последовательности представляет собой необходимое и достаточное условие её сходимости. ☼

♦ Утверждение 10.2. Всякая монотонная ограниченная последовательность сходится.

☼ Замечание 10.2. Отметим, что и для всех элементов неубывающей ограниченной сверху и невозрастающей ограниченной снизу последовательностей.

Заметим также, что не всякая сходящаяся последовательность монотонна, например: . ☼

10.2. Число Эйлера е.

Рассмотрим последовательность 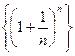. Покажем, что она является строго возрастающей и ограниченной. Применив формулу бинома Ньютона, получим:

,

.

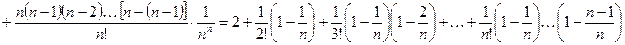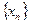При замене n на n +1 каждая скобка вида увеличивается (так как ) и добавляется одно положительное слагаемое. Поэтому и, следовательно, – строго возрастающая последовательность. Докажем её ограниченность.

Учитывая, что 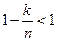(k =1,2,…, n –1) и что (n =3,4,…) получаем:

.

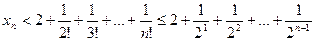Для 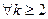справедливо неравенство , но тогда .

Используем формулу суммы первых k членов геометрической прогрессии 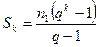и получим, что . Таким образом, , последовательность 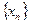– ограниченная, согласно утверждению 10.2 она имеет конечный предел. Этот предел определяет широко используемое в математике число е, которое называется эйлеровым числом:

.

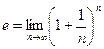Можно показать, что е – иррациональное число. Мы показали, что 2< e <3. С точностью до число е =2,718281828459045. Обычно в вычислениях используют е 2,72.

Определение 10.3. Бесконечную последовательность сегментов 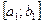, , 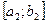, 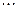назовём стягивающейся системой сегментов, есл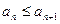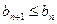и , и .

♦ Теорема 10.2. У всякой стягивающейся системы сегментов 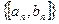существует, и притом единственная, точка с, принадлежащая всем сегментам этой системы.

Доказательство. Сначала докажем существование точки с.

Пусть – неубывающая последовательность; 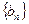– невозрастающая последовательность. Т.к. обе последовательности сходятся, то и последовательность также сходится, . Обозначим общий предел , причём , так как . То есть с существует и принадлежит всем сегментам.

Докажем теперь единственность точки с. Пусть точка d > c принадлежит всем сегментам. Тогда отрезок 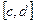тоже принадлежит всем сегментам и т.к. , то 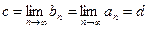, следовательно, с = d. Таким образом, точка, принадлежащая всем сегментам системы единственна. ■

Дата добавления: 2014-01-07