Недостатки механизмов с ВКП

Достоинства механизмов с ВКП

- Все механизмы с ВКП малозвенны, следовательно, позволяют уменьшать габариты машины в целом.

- Механизмы с ВКП более точно воспроизводят передаточную функцию.

- Обеспечивают большое разнообразие законов движения выходного звена.

- Механизмы с ВКП должны иметь силовое или геометрическое замыкание (зубчатые колеса – геометрическое, кулачковый механизм - силовое).

- Контактные усилия в ВКП гораздо выше, чем в НКП, что приводит к износу, т.е. 2 профиля теряют свою форму и как следствие, свое главное достоинство.

Угол давления в высшей паре

Угол давления – это угол между скоростью в точке контакта и нормалью к профилю (т.е. направление силы). Обычно этот угол обозначают 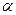или 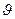. И в одной точке контакта два профиля имеют разный угол давления.

Учитывая, что мощность в ВКП передается по нормали, а по касательной – скольжение запишем формулу определения мощности

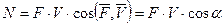
Если 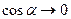, то 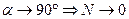- так называемое явление заклинивания, скорость есть, усилие есть, но ведомое звено не трогается с места. Т.е заклиниванием называется положение, при котором никакая по величине сила, приложенная к ведомому звену, не может привести его в движение.

Так как в процессе движения в реальных условиях участвуют разнообразные силы терния, то заклинивание наступает гораздо раньше, чем угол давления достигнет 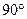. Поэтому в различных механизмах допустимый угол давления стандартизован и обозначается 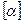или .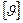

Основная теорема зацепления (теорема Виллиса)

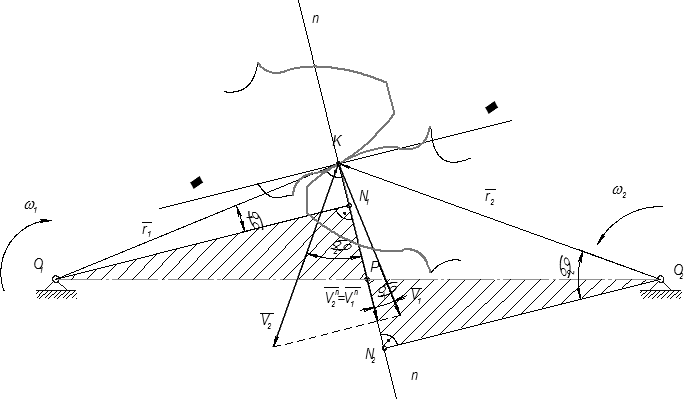Рассмотрим два тела 1 и 2, совершающих вращательное движение соответственно вокруг центров 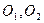с угловыми скоростями 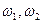образующие высшую КП.

1. Отметим на общей нормаль контактную точку .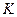

2. Проведем радиусы векторы точки для тел 1 и 2: .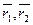

3. Определим скорость в контактной точке , .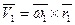

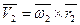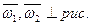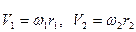4. Так как вектор , то и , .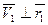

5. Опускаем соответствующие перпендикуляры на нормаль, и исходя из условия существования высшей КП : .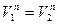

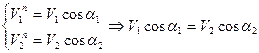6. .

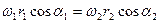7. 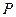- полюс зацепления – это точка пересечения линии центров с общей нормалью к профилям в точке контакта. Опустим перпендикуляры из центров 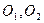на общую нормаль и отметим точки 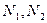: 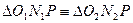(по третьему признаку подобия – по трем углам).

8. Как углы со взаимно перпендикулярными сторонам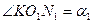и и 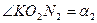, следовательно 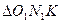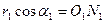из : , из : .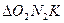

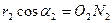9. 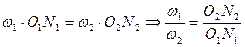, из подобия треугольников : ,

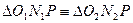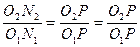10. Следовательно: 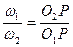Таким образом, полюс относительного вращения звеньев лежит на линии центров и делит ее на отрезки обратно пропорциональные угловым скоростям.

Теорема Виллиса. Передаточное отношение между звеньями, совершающими вращательное движение прямо пропорционально отношению угловых скоростей и обратно пропорционально отношению расстояний от центров вращения до полюса.

Равенство векторов скоростей по направлению для тел, совершающих вращательное движение, возможно только на линии соединяющей центры вращения тел. Поэтому полюс относительного вращения должен лежать на этой линии. Т.о. полюс – это единственная контактная точка, в которой отсутствует проскальзывание.

Формулировка анализа. Контактная нормаль к профилям высшей пары пересекает линию центров в полюсе относительного вращения звеньев.

Формулировка синтеза. Профили в высшей кинематической паре должны быть выполнены так, чтобы контактная нормаль к ним проходила через полюс относительного вращения звеньев.

Так как положение полюса на линии центров определяет передаточное отношение механизма, то профили удовлетворяющие основной теореме зацепления обеспечивают заданный закон изменения передаточного отношения или являются сопряженными.

Зубчатые передачи

Зубчатыми передачами называются механизмы с высшими кинематическими парами, в состав которых входят зубчатые колеса, рейки или секторы - звенья, снабженные профилированными выступами или зубьями. Зубчатые передачи бывают простые и сложные. Простая зубчатая передача - трехзвенные механизм, состоящий из двух зубчатых колес и стойки, в котором зубчатые колеса образуют между собой высшую пару, со стойкой - низшие (поступательные или вращательные).

Выбор параметров зубчатых передач обусловлен конструктивными и технологическими условиями.

Эвольвентная зубчатая передача

Эвольвентная зубчатая передача - цилиндрическая зубчатая передача, профили зубьев которой выполнены по эвольвенте окружности.

Эвольвента окружности и ее свойства

Эвольвента окружности - это плоская кривая, которая описывается точкой прямой при ее перекатывании по окружности, прямая при этом называется производящей, окружность – основной (базисной, отсюда и обозначение 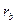). Т.е. эвольвента – это развертка окружности. Построение эвольвенты должно обеспечивать в любом положении равенство дуги окружности и прямой.

Дата добавления: 2014-01-07