Распределение Стьюдента

Служит для изучения вероятностных характеристик выборочных средних. Из того факта, что каждая выборка отбирается из генеральной

совокупности случайным образом, следует, что для распределения средних справедливо следующее:

1. Среднее значение распределения равно среднему в генеральной совокупности

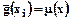
2. Его стандартное (среднеквадратичное) отклонение равно ,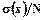

где 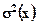– дисперсия исходной генеральной совокупности.

3. Его форма будет близкой к «колоколу» нормального распределения, если объемы выборок не слишком малы.

Эти положения хорошо подтверждаются опытом при обобщении эмпирически полученных выборочных распределений.

На практике нам не известны ни μ(х), ни σ²(х). По выборочным данным можно рассчитать только их оценк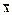и и 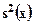. Эти данные не дают оснований считать, что выборочное распределение является нормальным со стандартным отклонением 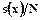(на самом деле его стан-

дартное отклонение неизвестно и равно 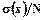). В таком случае воз-

никает проблема: как описать выборочное распределение?

Решение этой проблемы было дано в 1908г. У.Госеттом, который публиковал свои работы под псевдонимом «Стьюдент». Это было первым серьезным достижением в статистическом анализе малых выборок. Госетт показал, что статистика

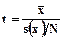(10.1)

подчиняется так называемому t-распределению (которое стали назы-вать распределением Стьюдента) с числом степеней свободы (ЧСС), равным ν. Это означает, что данное распределение зависит только от одного параметра – ν, который легко находится по объему выборки. Оно имеет очень сложную формулу плотности распределения

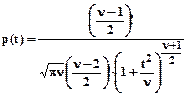(10.2)

где! – знак факториала.

Число степеней свободы – параметр, равный объему выборки минус число оцениваемых по этой выборке параметров.

Для t-распределения ЧСС ν = N-1.

График функции плотности t-распределения симметричен относительно оси ординат и с ростом ν приближаетсяк кривой нормального распределения (рис.10.2).При малых ν t- распределение заметно отличается от нормального своей большой рассеянностью значений относительно центра распределения. Для того, чтобы распределение

Стьюдента не слишком отличалось от нормального, объемы выборок

должны быть не очень малыми .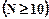

Рисунок 10.2 – Распределение Стьюдента

Это следует из того, что у нормального распределения 95% наблюдаемых значений заключено в интервале 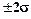, а для распределения Стьюдента при N =10 – в пределах 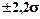. Т.о. даже для относительно небольших выборок расчет дисперсии по выборочным данным не может сильно исказить оценку математического ожидания.

Практическое значение распределения Стьюдента в том, что:

1. Найден точный ответ на вопрос о характере выборочного распределения средних для выборок небольшого объема.

2. Обосновано положение о том, что разница между распределением

средних и нормальным распределением невелика. Нормальное распределение может служить хорошей аппроксимацией даже в том случае, когда вместо 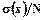приходится использовать .

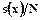3. Получена возможность выяснения вероятностных свойств выборочных средних, когда дисперсия 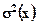неизвестна.

4. Статистика (8.1) может использоваться до отбора выборки для вы-

движения различных гипотез относительно выборочных средних, в частности, при интервальном оценивании.

10.3 Распределение 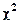(хи-квадрат)

Это распределение, называемое также распределением Пирсона, используется при изучении вероятностных свойств выборочных дисперсий.

Если s²(x) – дисперсия случайной величины по выборке из генеральной совокупности с дисперсией σ²(х) и неизвестным μ(х), то статистика

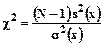(10.3)

подчиняется так называемому χ² – распределению с единственным параметром ν = N-1.

Распределение хи-квадрат возникает при рассмотрении случайной величины

,

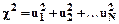где 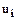- независимые нормально распределенные случайные величины

с μ(u) = 0 и σ²(u) = 1.

Функция плотности распределения χ² , подобно функции плотности t-распределения, имеет очень сложную структуру

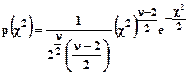(10.4)

Графики функции плотности этого распределения показаны на рисун-

ке 10.3:

Рисунок 10.3 – Распределение χ²

По рисунку 10.3 видно, что с ростом объема выборки χ²- распределение очень быстро становится похожим на нормальное. Область определения функции р(χ²) – от 0 до + ∞. При малых ЧСС она асимметрична, но с ростом ν она становится более пологой и симметричной. При N → ∞ распределение стремится к нормальному с параметрам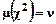и

и .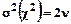

Распределение хи-квадрат применяется для описания вероятностных свойств эмпирических дисперсий. При помощи статистики (10.2) можно осуществлять интервальное оценивание эмпирической дисперсии s²(х), если до опыта известно σ²(х), а μ(х) – неизвестно

,

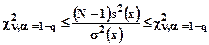где 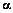- уровень значимости критерия (см. лекцию № 9).

Дата добавления: 2014-01-07