Обращение теоремы Лагранжа

Теорема Лагранжа утверждает, что если 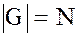, a , то

,

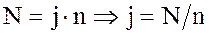т.е. порядок 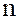любой подгруппы H группы G делит N – порядок группы G.

Естественно, возникает вопрос об обращении теореме: если m является делителем 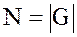, то существует ли в группе G подгруппа H порядка m?

Другими словами: существует ли для каждого делителя m порядка группы N подгруппы H группы G порядка m?

В общем случае ответ отрицательный, однако в некоторых частных случаях такое обращение теоремы Лагранжа справедливо.

Теорема. (обращение теоремы Лагранжа)

1. Всякая подгруппа циклической группы есть снова циклическая группа.

2. Подгруппы бесконечной циклической группы 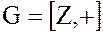исчерпываются бесконечными группами .

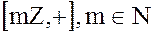3. Подгруппы циклической группы порядка 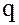находятся во взаимно однозначном соответствии с положительными делителями 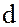числа .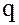

Доказательство.

Докажем 1. Пусть 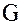– произвольная циклическая группа порядка . Для определенности будем предполагать, что 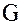– аддитивная группа.

В этом случае общий элемент группы 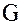имеет вид

.

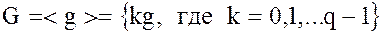Пусть – произвольная неединичная подгруппа группы 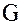, т.е. .

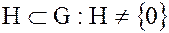Так как 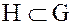, то элементами подгруппы являются элементы вида 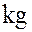, но если .

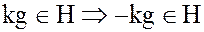Среди всех элементов вида , выберем элемент

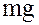, где 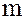– наименьшее положительное число.

Тогда любое можно представить в виде:

.

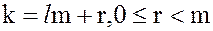Из того, что

,

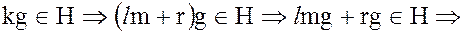
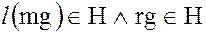но m – наименьшее число, удовлетворяющее условию

mgÎH Þ r = 0 Þ H =<mg>,

т.е. Н – циклическая группа с образующим элементом mg.

Докажем 2. Подгруппы бесконечной циклической группы 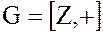исчерпываются бесконечными группами .

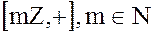Действительно, так как 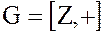– циклическая группа с образующим элементом 1 или 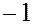, т.е.

,

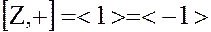то, в соответствии с пунктом 1 данной теоремы, любая подгруппа H циклической группы 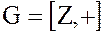определяется натуральным числом 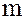и имеет вид

,

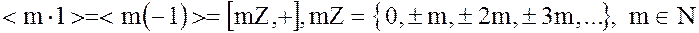причем все эти подгруппы бесконечны.

Докажем 3. Подгруппы циклической группы порядка 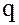находятся во взаимно однозначном соответствии с положительными делителями 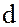числа .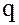

Пусть, как и ранее, 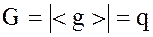– аддитивная циклическая группа порядка 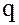, т.е.

.

Если 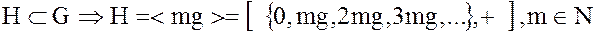, причем, если элемент

.

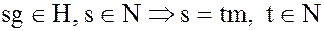Нам надо доказать, что 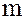делит .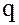

Действительно, представим

.

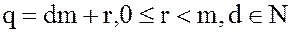Тогда из того, что

,

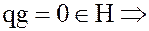
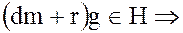
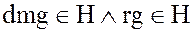а минимальность 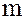влечет , следовательно .

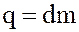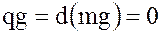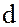Таким образом, из того, что , следует, что подгруппа имеет порядок , т.е.

.

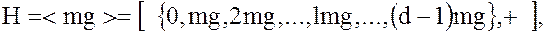
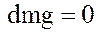Когда 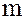пробегает по всем положительным делителям числа 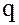, то же самое делает и 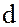, и мы получаем ровно по одной подгруппе порядка 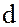, делящего .

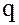Следствие. В циклической группе порядка 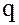подгруппа 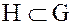порядка 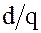совпадает с множеством элементов 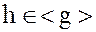, таких, что .

Доказательство. Элементы циклической группе порядка 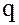имеют вид

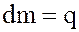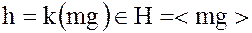Если , то и .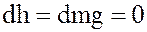

Обратно, пусть 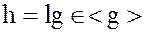и .

Из условия 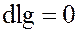следует, что 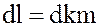, откуда 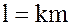и .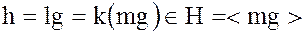

Дата добавления: 2014-01-07