Простой динамический анализ

Обзор базовых методов прогнозирования

Каждое значение временного ряда может состоять из следующих составляющих: тренда, циклических, сезонных и случайных колебаний. Метод простого динамического анализа используется для определения тренда имеющегося временного ряда. Данную составляющую можно рассматривать в качестве общей направленности изменений значений ряда или основной тенденции ряда. Циклическими называются колебания относительно линии тренда для периодов свыше одного года. Такие колебания в рядах финансовых и экономических показателей часто соответствуют циклам деловой активности: резкому спаду, оживлению, бурному росту и застою. Сезонными колебаниями называются периодические изменения значений ряда на протяжении года. Их можно вычленить после анализа тренда и циклических колебаний. Наконец, случайные колебания выявляются путем снятия тренда, циклических и сезонных колебаний для данного значения. Остающаяся после этого величина и есть беспорядочное отклонение, которое необходимо учитывать при определении вероятной точности принятой модели прогнозирования.

Метод простого динамического анализа исходит из предпосылки, что прогнозируемый показатель (Y) изменяется прямо (обратно) пропорционально с течением времени. Поэтому для определения прогнозных значений показателя Y строится, например, следующая зависимость:

(1),

где t - порядковый номер периода.

Параметры уравнения регрессии (a, b) находятся, как правило, методом наименьших квадратов. Существуют также другие критерии адекватности (функции потерь), например метод наименьших модулей или метод минимакса. Подставляя в формулу (1) нужное значение t, можно рассчитать требуемый прогноз.

Авторегрессионые зависимости

В основу этого метода заложена достаточно очевидная предпосылка о том, что экономические процессы имеют определенную специфику. Они отличаются, во-первых, взаимозависимостью и, во-вторых, определенной инерционностью. Последняя означает, что значение практически любого экономического показателя в момент времени t зависит определенным образом от состояния этого показателя в предыдущих периодах (в данном случае мы абстрагируемся от влияния других факторов), т.е. значения прогнозируемого показателя в прошлых периодах должны рассматриваться как факторные признаки. Уравнение авторегрессионой зависимости в наиболее общей форме имеет вид:

(2),

где Y_t - прогнозируемое значение показателя Y в момент времени t;
Y_t-i - значение показателя Y в момент времени (t-i);
A_i - i -й коэффициент регрессии.

Достаточно точные прогнозные значения могут быть получены уже при k = 1. На практике также нередко используют модификацию уравнения (2), вводя в него в качестве фактора период времени t, то есть объединяя методы авторегрессии и простого динамического анализа. В этом случае уравнение регрессии будет иметь вид:

(3)

Коэффициенты регрессии данного уравнения могут быть найдены методом наименьших квадратов. Соответствующая система нормальных уравнений будет иметь вид:

(4)

где j - длина ряда динамики показателя Y, уменьшенная на единицу.

Для характеристики адекватности уравнения авторегрессионой зависимости можно использовать величину среднего относительного линейного отклонения:

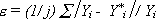
(5),

где Y^*_i - расчетная величина показателя Y в момент времени i;
Y_i - фактическая величина показателя Y в момент времени i.

Если e < 0,15, считается, что уравнение авторегрессии может использоваться при определении тренда временного ряда экономического показателя в прогнозных целях. Ввиду простоты расчета критерий e достаточно часто применяется при построении регрессионных моделей.

Дата добавления: 2014-01-07