Параметры эвольвентного зубчатого колеса

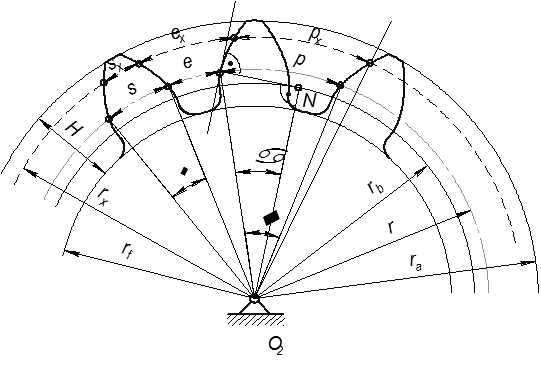
Существует три параметра зубчатого колеса, которые можно определить «на глаз» при наличии этого зубчатого колеса и 2 которые можно только рассчитать.

1. Число зубьев колеса 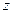, можно подсчитать по готовому колесу (при проектировании этим параметром задаются).

2. Окружность вершин, окружность впадин 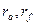. При наличии колеса могут быть измерены, например, штангенциркулем. Окружность вершин – это окружность, ограничивающая зуб со стороны противоположной телу колеса. Окружность впадин – это окружность, ограничивающая зуб со стороны тела колеса. Зная эти окружности можно получить высоту зуба колеса: .

3. Для получения эвольвентного профиля необходимо знать расположение основной окружности колеса 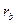- рассчитывается.

4. Делительная окружность 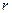– делит зуб на ножку зуба и головку зуба. Делительной окружностью называется окружность стандартного шага, модуля и угла давления (или окружность, проходящая через точку эвольвенты для которой профильный угол ).

5. Модулем зацепления называется линейная величина в p раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к p. В зависимости от окружности, по которой определен модуль, различают делительный, основной, начальный. Для косозубых колес еще и нормальный, торцевой и осевой модули. В ряде стран используется величина обратная модулю, которая называется питчем. Питч (диаметральный) - число зубьев колеса, приходящееся на дюйм диаметра. Исходя из этого, модуль можно определить как число миллиметров диаметра, приходящееся на один зуб. На колесе можно провести бесчисленное число окружностей, на каждой из которых будет свой модуль. Для ограничения этого числа ГОСТом введен стандартный ряд модулей. Стандартной модуль определяется по делительной окружности .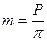

6. Окружным шагом, или шагом, называется расстояние между одноименными точками профилей двух соседних зубьев, измеренное по дуге любой окружности (под одноименными понимаются правые или левые профили зуба). Обозначается . Достаточно часто вводится понятие углового шага - центральный угол, соответствующий дуге окружного шага по делительной окружности. Шаг колеса делится на толщину зуба 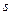и ширину впадины 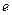: . Толщина зуба 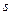- расстояние по дуге соответствующей окружности между разноименными точками профилей зуба. Ширина впадины 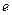- расстояние по дуге соответствующей окружности между разноименными точками профилей соседних зубьев.

7. - угловая толщина зуба. 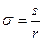- центральный угол соответствующий дуге.

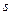8. 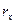- окружность произвольного радиуса.

Дата добавления: 2014-01-07