
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы расчета
|
|
|
|
Типы задач в теории размерных цепей.
Расчет и анализ размерных цепей является обязательным этапом при конструировании машины. Он обеспечивается взаимозаменяемость способствует повышению качества и снижению трудоемкости изготовление машины.
Сущность решения размерной цепи – установить допуски и отклонения всех размеров исходя из конструкции и технологии. При этом встречаются задачи двух типов:
1) Технологическая (или проверочная) – определить номинальный размер АΔ и его предельные отклонения по заданным номинальным размерам Аj и их предельным отклонениям (проверочный расчет допусков чертежа, технологическая задача).
2) Конструкторская (прямая) задача – назначить предельные размеры составляющих звеньев (части их) по заданным предельным размерам (замыкающего) звена (задача проектного расчета размерной цепи).
Основное требование к решению – технологическая выполняемость назначенных допусков.
1) На максимум-минимум (обеспечивает полную взаимозаменяемость).
2) Вероятностный метод.
3) Групповой взаимозаменяемости.
4) Метод регулирования.
5) Метод пригонки.
Методы 2–5 – неполная (частичная) взаимозаменяемость.
- Метод максимума-минимума.
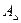 – замыкающий размер;
– замыкающий размер;
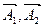 – увеличивающие;
– увеличивающие;
 – уменьшающие.
– уменьшающие.
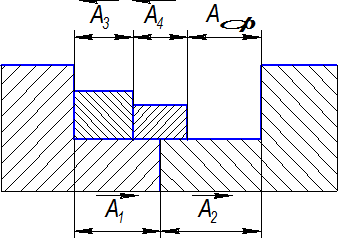
Цепь замкнута: сумма номинальных размеров по одной ветви графика должна быть равной сумме номинальных размеров по другой ветви:
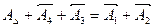
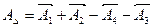
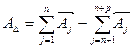 (1)
(1)
где n – увеличивающих размеров;
р – уменьшающих звеньев;
m – всего звеньев;
n+p = m–1
Размерную цепь можно считать по предельным размерам и его предельным отклонениям.
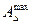 можно получить, если звенья 3 и 4 взять по наибольшему предельному размеру, а 1 и 2 – по наименьшему.
можно получить, если звенья 3 и 4 взять по наибольшему предельному размеру, а 1 и 2 – по наименьшему.
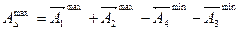

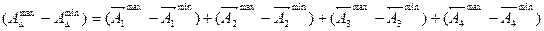
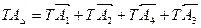
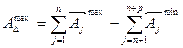 (2)
(2)
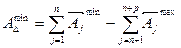 (3)
(3)
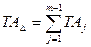 (4)
(4)
Выводы:
1. В качестве замыкающего выбирать менее точный (неответственный) размер.
2. Стремится к минимуму составляющих звеньев в размерной цепи.
Определим предельные отклонения замыкающего звена:
(2)–(1)
 (5)
(5)
(3)-(4)
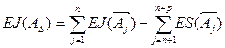 (6)
(6)
Проверочные (технологические) задачи относительно параметров АΔ решаются с помощью приведенных 6-ти уравнений.
В большинстве случаев при конструировании заданы размеры замыкающего звена, а необходимо определить допуски и размеры составляющих звеньев.
Здесь 6-ти уравнений недостаточно, надо дополнительно задаться какими-то условиями.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 311; Нарушение авторских прав?; Мы поможем в написании вашей работы!