ЛЕКЦИЯ 14. Физические процессы в вакууме

ЧАСТЬ 2

(физика вакуума-3)

Содержание

Физические процессы в вакууме

1. Вязкость газов

2. Перенос тепла

3. Диффузия в газах

4. Температурное равновесие давлений

5. Испарение, конденсация, хемосорбция как поверхностные процессы

Приложение

Рис. 14.7. Изобары сорбции водорода на никелевом порошке (рис. 6.16, Дешман С. Научные основы вакуумной техники)

Рис. 14.8. Изотермы сорбции водорода на никеле и меди (рис. 6.17, Дешман С. Научные основы вакуумной техники)

ФИЗИЧЕКИЕ ПРОЦЕССЫ В ВАКУУМЕ

1. Вязкость газов. Газ, текущий по трубопроводу, испытывает сопротивление вследствие трения о стенки, и поэтому скорость потока равномерно уменьшается в направлении от центра трубы, причем у стенок она становится равной нулю. Каждый слой газа, параллельный направлению потока, действует с некоторой тангенциальной силой на соединение слои. Эта сила, направленная параллельно потоку, стремится уменьшить скорость более быстро движущегося слоя и увеличить скорость более медленного слоя. Это явление называется внутренним трением, или вязкостью.

В качестве рабочей гипотезы можем предположить, следуя Ньютону, что внутреннее трение прямо пропорционально градиенту скорости в газе. Кроме того, вязкость должна зависеть от природы текущей среды. Таким образом, приходим к следующему определению коэффициента вязкости. Коэффициентом вязкости называется тангенциальная сила (сила внутреннего трения), действующая на единицу площади внутри жидкости, когда уменьшение скорости с расстоянием равно единице (т.е. когда градиент скорости равен единице).

Пользуясь этим определением, мы можем найти соотношение между коэффициентом вязкости и средней длиной свободного пути молекул в газе.

Обозначим через U скорость потока газа на расстоянии d от неподвижной стенки (поверхности). В стационарном потоке, направленном вдоль стенки, скорость будет равномерно уменьшаться до нуля по мере приближения к этой поверхности. Эта ситуация представлена на рис. 1. Скорость на расстоянии d равна U и представлена ординатой АВ, а скорости на меньших расстояниях представлены ординатами точек, лежащими на прямой ОВ.

Представим себе, что газ разделен на слои, параллельные поверхности, причем толщина каждого слоя равна длине свободного пути молекулы L. Обозначим через В тангенциальную силу (силу трения), действующую на единицу площади между соседними слоями. По данному (Ньютоном) определению В = m×(градиент скорости), или 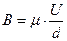, где m - динамический коэффициент вязкости. (1)

Согласно кинетической теории, сила терния, действующая на единичную площадку, измеряется скоростью переноса количества движения через единицу площади между двумя смежными слоями (площадка F на рис. 14.1).

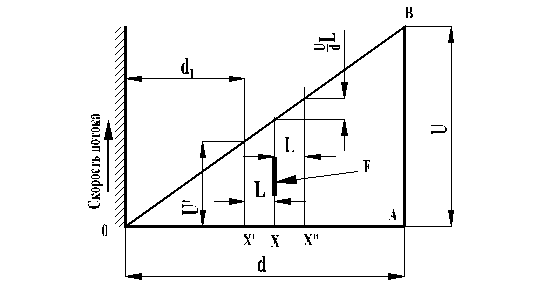
Рис.14.1. Расчетная схема для определения коэффициента вязкости в газах при низком вакууме

В плоскости х₀ (рис.1) происходит столкновение молекул, вылетивших из плоскостей х¢ и х¢¢. В результате одного столкновения количество движения в слое х₀ изменится на величину 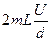. Но в единицу времени к единице площади в сторону х₀ от плоскостей х¢ и х¢¢ пойдут равные потоки . Эти потоки образуют N_q столкновений (молекула с молекулой). Таким образом, общее изменение количества движения в плоскости х₀ в единицу времени на единичной площадке составит 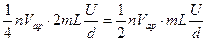. 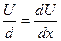Но - градиент скорости в направлении от стенки. Тогда с учетом определения (1)

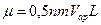, (2)

где n – концентрация газа в потоке, m - масса молекулы, V_ap - среднеарифметическая скорость молекул.

Более точные расчеты определяют 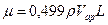, где r - плотность газа (r = m×n).

Учитывая, что 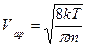, , 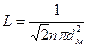из (2) получим .

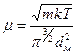Видим, что природа газа учитывается параметрами m и d_м.

Рассмотрим подробнее зависимость 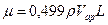. Из этого соотношения можно сделать интересный вывод о зависимости вязкости от давления. Так как L обратно пропорциональна n, а r - прямо пропорциональна, то Lr от концентрации газа не зависит, а т.к. P = nkT, то при постоянной температуре вязкость любого газа от давления не зависит и должна увеличиваться с температурой. При сверхвысоком, высоком и среднем вакууме (т.е. тогда, когда наблюдается эффект скольжения: скорость молекул газа на стенке ¹0) вывод о независимости вязкости от давления экспериментально не подтверждается.

Если определить градиент скорости не как U/d, а как U/(d₁+2L), что сужает область проявления эффектов, связанных с тернием (например, область пограничного слоя), то можно провести следующий анализ. В области низкого вакуума, когда d₁>>2L, распределение скоростей линейное (как на рис.1), а dU/dx = const. Сила трения в этом случае от давления не зависит, m = const. В области среднего вакуума, когда d₁» L градиент скорости уменьшается (начинает играть роль проскальзывание), сила трения уменьшается по мере снижения давления. В высоком вакууме силу трения (когда величиной d₁ можно пренебречь) можно определить по выражению

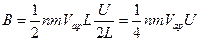. (3)

Таким образом, сила трения в области высокого и сверхвысокого вакуума пропорциональна молекулярной концентрации или давлению газа. Проведенный анализ объясняет качественную картину зависимости динамического коэффициента вязкости от давления при различных степенях вакуума.

2. Перенос тепла. Передача теплоты (тепла) в разреженных газах (как уже отмечалось в данном лекционном курсе) может происходить за счет трех процессов: конвекции, теплопроводности (кондукции) и излучения. Конвективный теплообмен может быть естественным (естественная конвекция) и вынужденным, при наличии нестационарных газовых потоков во время начальной откачки вакуумных камер, т.е. на переходном процессе вакуумирования. При низком вакууме конвективный теплообмен является основным способом теплопередачи. В области среднего и высокого вакуума роль конвективного теплообмена в общем тепловом балансе мала, и этим видом теплообмена в расчетах обычно пренебрегают.

Теплопередача за счет теплопроводности в вакууме может рассматриваться как явление переноса. Этот процесс характеризуется количеством тепла, переносимым одной молекулой газа: C_vmT, где 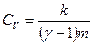, , 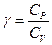m – масса молекулы.

Рассмотрим аналогично переносу количества движения перенос тепла между двумя пластинами, температуры которых равны Т₁ и Т₂ (рис. 14.2).

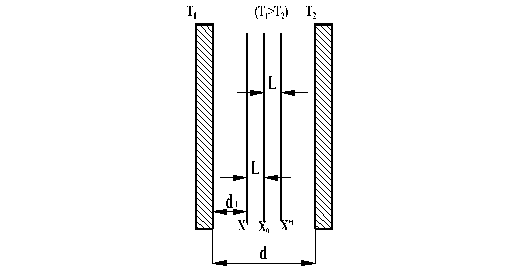
Рис.14.2. Схема процесса переноса тепла для расчета коэффициента теплопроводности

Как и в случае определения коэффициента вязкости рассмотрим два слоя газа толщиной L, заключенные между пластинами, температуры которых равны Т₁ и Т₂ (пусть Т₁ > Т₂). Пластины расположены друг от друга на расстоянии d. Падение температуры между плоскостями х¢ и х¢¢ будет линейным и равным .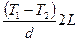

Тогда количество тепла, переносимое газом через единицу площади в единицу времени, равно

,

или

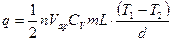, (4)

где 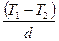- градиент температуры: .

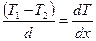Выражение (4) можно представить в форме закона Фурье: 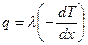. Но 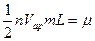. Зависимость (4) может быть представлена в следующей форме 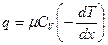, сопоставляя это выражение с законом Фурье, получим

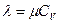. (5)

Как и в случае вывода соотношения для m, более тщательное рассмотрение механизма переноса энергии молекулами приводит к выражению

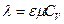, (6)

где 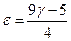; 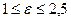в зависимости от атомности газа.

Из выражения (6) следует вывод, что качественная зависимость l от степени вакуума аналогична таковой для m.

Коэффициент аккомодации. Когда молекулы газа, находящегося первоначально при температуре T_i, сталкиваются с поверхностью нагретой стенки, температура которой T₁ (T₁>T_i), то при первом столкновении полного обмена энергией не наступает. Поэтому Кнудсеном была введена некоторая константа, названная коэффициентом аккомодации. Обозначим ее через a. Кнудсен определил этот коэффициент как «величину, указывающую насколько полно молекулы, сталкивающиеся с поверхностью, а затем отраженные ею, успевают при столкновении приобрести ту среднюю энергию, которая соответствует температуре нагретой поверхности».

Молекулы, отражающиеся (или испускаемые) от нагретой поверхности, обладают поэтому (т.к. не успели обменяться энергией полностью) средней энергией, которая соответствует температуре T_r, меньшей Т₁. Следовательно, коэффициент аккомодации можно определить соотношением

. (7)

При a = 1 температура T_r = Т₁; если a < 1, то T₁>T_r>T_i.

Анализ на основе кинетической теории газов показывает, что средняя энергия, переносимая молекулой с поверхности, имеющей температуру Т, выражается равенством E = 2kT (вместо 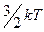- средняя энергия молекул газа в объеме).

Учитывая коэффициент аккомодации, градиент температуры необходимо выразить в следующей форме

,

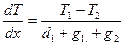где ; ;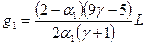

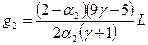a₁ и a₂ – коэффициенты аккомодации поверхностей переноса.

Диффузия в газах. Уравнение стационарной диффузии, согласно закону Фика, имеет следующий вид

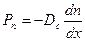, (8)

где Р_п – плотность потока частиц в направлении, противоположном градиенту концентрации, D_c – коэффициент самодиффузии, dn/dx – градиент концентрации. Рассмотрим однородный газ. В условиях вакуума через плоскость, перпендикулярную потоку молекул, с обеих сторон из слоев, удаленных от плоскости на расстояние L₀ (рис.14.3) будут проходить (через единичную площадку в единицу времени) два встречных потока N_q.

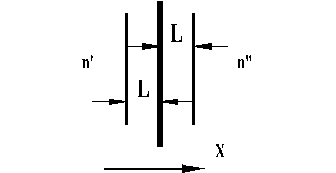
Рис.14.3. Схема процесса диффузии

Разность этих потоков и определяет скорость диффузии

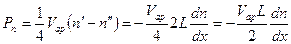, (9)

где n¢ и n¢¢ - концентрация газа в слоях, удаленных от рассматриваемой плоскости на L.

Сравнивая выражения (8) и (9), получим

,

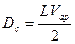или, воспользовавшись выражениями для V_ap и L,

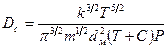. (10)

Здесь С – постоянная Сезерленда, входящая в выражение для определения L.

Таким образом, коэффициент диффузии (самодиффузии) в области низкого вакуума пропорционален давлению. Температурный фактор в выражении (10) можно представить в форме Т^х, где х меняется от 1,5, при T>>C, до 2,5, при T<<C. Видим, что коэффициент самодиффузии увеличивается с повышением температуры.

В области высокого вакуума L больше эффективного размера системы, в которой происходит процесс. Поэтому в выражении (9) вместо 2L надо поставить l _эф. Тогда

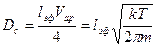. (11)

Видим, что D_c в высоком вакууме не зависит от давления.

На рис. 14.4 представлена зависимость коэффициентов переноса от давления при различных степенях вакуума.

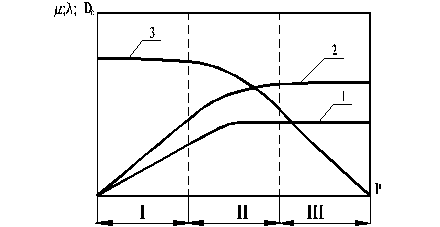
Рис. 14.4. Зависимость коэффициентов переноса от давления: 1 - m; 2 - l; 3 – D_c; I – высокий вакуум; II – средний; III – низкий

Термодиффузия. Явление термодиффузии описывается следующим образом. Если в смеси двух газов однородной концентрации создать градиент температуры, то более тяжелые и крупные молекулы (массой m₁ и диаметром d₁) обнаруживают тенденцию двигаться в сторону понижения температуры, а более легкие и меньшего размера – в направлении повышения температуры. Разделяющий эффект характеризуется коэффициентом термодиффузии D_T. Процессы термодиффузии и самодиффузии протекают одновременно (параллельно), в результате чего устанавливается равновесное (стационарное) состояние, при котором градиент концентрации приходит в соответствие с температурным градиентом. Процесс характеризуется коэффициентом разделения при термодиффузии, являющимся отношением коэффициента термодиффузии и коэффициента самодиффузии

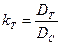, (12)

и степенью разделения 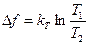, где T₁>T₂.

На рис.14. 5 и 14.6 показана зависимость степени разделения при термодиффузии для смеси H₂-N₂.

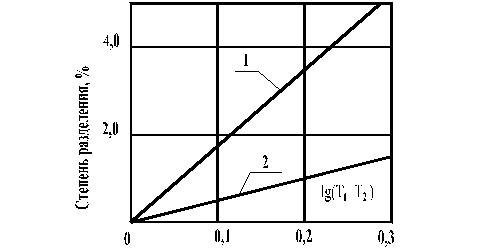
Рис.14.5. Зависимость степени разделения от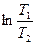

1 – смесь H₂-N₂ (50% H₂);

2 – смесь H₂-N₂ (5% H₂)

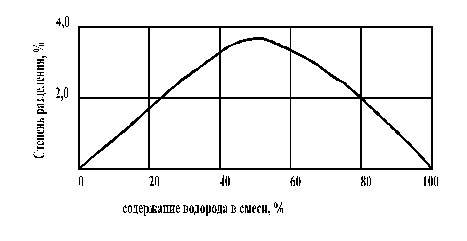
Рис.14.6. Зависимость 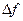от состава смеси H₂-N₂ при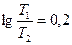

4. Температурное равновесие давлений. В связанных между собой сосудах, имеющих различную температуру, в зависимости от степени вакуума будет устанавливаться различное отношение давлений, а, следовательно, и молекулярных концентраций, т.к. P = nkT.

При низком вакууме условием равновесия в двух соединенных между собой объемах, имеющих различную температуру, будет установление равенства давлений: Р₁ = Р₂. При этом n₁/n₂ = T₂/T₁.

В высоком вакууме может установиться только динамическое равновесие, при котором равны потоки газа, переходящие из одного сосуда в другой, т.е. Nq₁=Nq₂.

Рассмотрим это равенство:

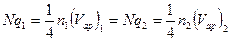. Но .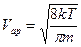

Тогда 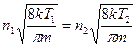, или .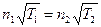

Отсюда следует: 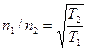, а также .

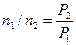Окончательно можно записать .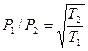

Эти соотношения справедливы для сосудов, соединенных между собой как отверстием, так и трубопроводом. Таким образом, в высоком вакууме равновесие в соединенных объемах устанавливается при давлениях, пропорциональных корню квадратному из отношения абсолютных температур.

В области среднего вакуума для определения соотношения между давлениями можно пользоваться приближенной формулой

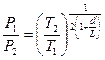, (13)

где d - характерный (эффективный) размер (диаметр) соединительного отверстия или трубопровода, L – средняя длина свободного пути молекулы при среднем давлении.

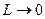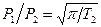Формула (13) дает значение Р₁ = Р₂ в области низкого вакуума (когда ) и в области высокого вакуума (когда ).

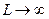Приведенные соотношения очень важны при измерении давления в вакуумных камерах, имеющих неравномерную (неоднородную) температуру газа.

Поясняющие примеры. Пусть манометрический преобразователь установлен на участке вакуумной системы с температурой Т₁ = 293К, а давление необходимо измерить в объеме вакуумной камеры, где температура T₂=77K (такие условия имеют место в вакуумных системах с криоконденсационными насосами, криогенными экранами). Тогда согласно (3) при высоком вакууме 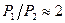. При измерении же давления в вакуумной печи при Т₂ = 1273К манометрическим преобразователем (датчиком), установленным на участке вакуумной системы, имеющей комнатную температуру Т₁ = 293К, .

Таким образом, без учета поправок на температурное равновесие легко ошибиться при измерениях давления при высоком вакууме (в два раза по условиям рассмотренных примеров).

Дата добавления: 2014-01-07