Семейство методов Рунге-Кутты. Методы второго порядка

Недостатком исправленного метода Эйлера (16) и других методов более высоких порядков, основанных на пошаговом представлении решения у(x) задачи (1)-(2) по формуле Тейлора и последовательном дифференцировании уравнения (1) для получения тейлоровых коэффициентов, является необходимость вычисления на каждом шаге частных производных функции f(x, y).

Идея построения явных методов Рунге-Кутты p-го порядка заключается в получении приближений к значениям f(x_i+1) по формуле вида

y_i+1 = y_i + hj(x_i, y_i, h), (17)

где φ(x, у, h) — некоторая функция, приближающая отрезок ряда Тейлора (12) до p-го порядка и не содержащая частных производных функции f(x, у).

Так, полагая в (17) j(x, y, h) = f(x, y), приходим к методу Эйлера (14.8), т.е. метод Эйлера можно считать простейшим примером методов Рунге-Кутты, соответствующим случаю p = 1.

Для построения методов Рунге-Кутты порядка, выше первого, функцию φ(x, у, h) берут многопараметрической, и подбирают ее параметры сравнением выражения (17) с многочленом Тейлора для у(x) соответствующей желаемому порядку степени.

Рассмотрим случай p = 2. Возьмем функцию φ в (17) следующей структуры:

φ(x, у, h) = c₁f(x, у) + c₂f(x + ah, у + bhf(x, у)).

Ее параметры c₁, c₂, a и b будем подбирать так, чтобы записанная, согласно (17), формула

y_i+1 = y_i + h(c₁f(x_i, y_i) + c₂f(x_i +ah, y_i + bhf(x_i, y_i))) (18)

определяла метод второго порядка, т. е. чтобы максимальная локальная ошибка составляла величину O(h³).

Разложим функцию двух переменных f(x + ah, у + bhf(x, у)) по формуле Тейлора, ограничиваясь линейными членами:

f(x + ah, y + bhf(x, у)) = f(x, у) + f'_x(x, y)ah + f'_y(x,y)bhf(x, y) + O(h²).

Ее подстановка в (18) дает

y_i+1 = y_i + h((c₁ + c₂)f(x_i, y_i) + h(c₂af'_x(x_i, y_i) +

+ c₂bf'_y(x_i, y_i)f(x_i, y_i))) + O(h³). (19)

Сравнение последнего выражения с тейлоровым квадратичным представлением решения у(x) (13) с точностью до O(h³) равносильно сравнению его с выражением y_i+1 по формуле (16), т.е. с исправленным методом Эйлера. Очевидно, чтобы (19) и (16) совпадали с точностью O(h³), от параметров нужно потребовать выполнение следующей совокупности условий:

(20)

Полученная система условий содержит три уравнения относительно четырех параметров метода. Это говорит о наличии одного свободного параметра. Положим с₂ = a (¹0). Тогда из (20) имеем:

c₁ = 1 – a, .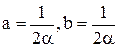

В результате подстановки этих значений параметров в формулу (18) приходим к однопараметрическому семейству методов Рунге-Кутты второго порядка.

. (21)

Выделим из семейства методов (21) два наиболее простых и естественных частных случая:

при получаем формулу

,

в котором узнаём метод Хойна (8), полученный ранее из других соображений;

при a = 1 из (21) выводим новый простой метод

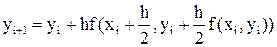, (22)

который назовем методом средней точки.

Дата добавления: 2014-01-07