Диаграммы состояния трехкомпонентных систем

Лекция 8-9

Список использованной и рекомендованной литературы

Основная

1. Канке В.А.. Философия. Исторический и систематический курс: Учебник для вузов. - М.: Логос, 2004.

2. Философия: Учебник / Под ред. В.Д. Губина. - М., 2003.

3. Философия: Учебное пособие для вузов. Ч.2. Основные проблемы философии / Под ред. В.И. Кириллова, С.И. Попова, А.Н. Чумакова.-2-е изд., перераб. и доп. - М.: Юристъ, 2002.-304 с.

4. Философия: Учебное пособие / Под ред. В.Н. Лавриненко. - М.: Юристъ, 2003.

Дополнительная

1.Философский энциклопедический словарь. - М.: ИНФРА-М, 2003

2.Философия: Учебник для вузов / Отв.ред. В.П. Кохановский. – Ростов н/Дону: Феникс, 2003

3.Социальная философия. - М., 2003

4.Крапивенский С.Э. Социальная философия. - Волгоград, 2003

Используемые в технике материалы очень часто содержат больше двух компонентов, поэтому нужен способ представления фазовых диаграмм более сложных систем.

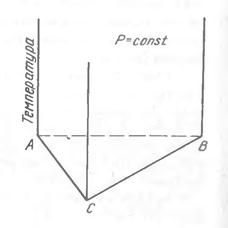
В трехкомпонентной системе, согласно правилу фаз Гиббса, максимальное число сосуществующих фаз Ф=4. В области существования одной гомогенной фазы К=3. Переменными величинами являются p, T, c₁,с₂. Обычно p=const, поэтому остаются три параметра: T, c₁,с₂. Для построения диаграммы состояния необходимы 3 оси координат, по которым можно было бы откладывать T, c₁,с₂. Тогда с₃ надо определять по разности, а это неудобно.

Чтобы избежать неудобств, используют прием, предложенный Гиббсом. От основан на геометрических свойствах правильных треугольников.

Зависимость свойств системы от трех переменных изображают в виде пространственной диаграммы, представляющей собой трехгранную прямоугольную призму. В основании призмы – равносторонний треугольник, характеризующий состав тройной системы (концентрационный треугольник), а высотой служит температура. Вершины равностороннего треугольника соответствуют чистым веществам А, В и С. Стороны АВ, ВС и СА служат для изображения составов соответствующих двойных систем. Все точки, расположенные внутри треугольника, выражают составы трехкомпонентных систем. Содержание каждого из компонентов тем больше, чем ближе расположена данная точка к соответствующей вершине. Концентрации компонентов выражают в масс.% или в мольных долях. Соответственно, каждая сторона концентрационного треугольника принимается равной 100% или 1.

Для определения состава трехкомпонентной системы используют два способа, предложенные Гиббсом и Розебумом.

Треугольник Гиббса. Этот способ определяется тем, что сумма перпендикуляров, опущенных из любой точки внутри треугольника на его стороны, равна высоте этого треугольника. Высота соответствует 100% какого-либо из компонентов. Из интересующей нас фигуративной точки М на каждую из сторон треугольника опускают перпендикуляры. Сумма их длин Ма+Мв+Мс=100%, а содержание компонентов A, В и С пропорционально длинам отрезков Ма, Мв и Мс (каждый отрезок лежит напротив вершины, отвечающей соответствующему компоненту). Таким образом и определяют содержание каждого из компонентов. В нашем примере точка М соответствует составу А 20%, В 50%, С 30%.

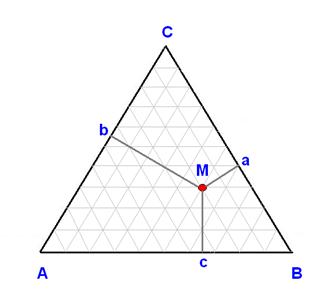
Треугольник Гиббса

Треугольник Розебома. В этом способе за 100% принимают сторону треугольника и наносят сетку линий, параллельных каждой стороне. Сумма отрезков таких линий, исходящих из фигуративной точки М и кончающихся на сторонах треугольника, есть постоянная величина, равная любой из сторон. Для точки М проекции этих отрезков на стороны треугольника Ab’, Ca’ и Вс’ дают процентное содержание каждого из компонентов: А 20%, В 50%, С 30%.

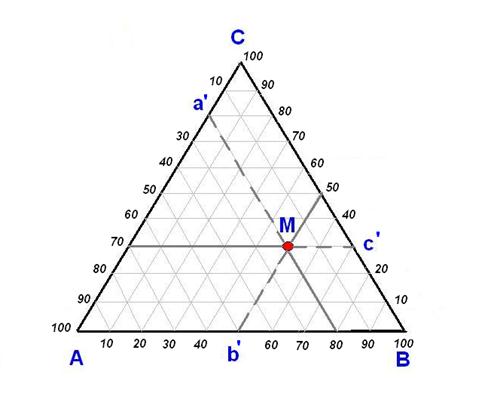
Треугольник Розебома

Можно видеть, что состав смеси в том и другом способе представления оказался идентичен.

Далее будем использовать треугольник Розебома.

Отметим три важных свойства линий (проекций) внутри треугольника Розебома.

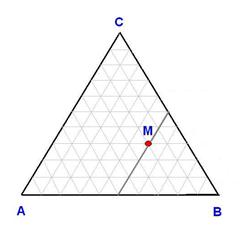
1) Линии, параллельные одной из сторон треугольника, представляют собой геометрические мести точек, соответствующих ряду смесей с одинаковым содержанием компонента, характеризуемого вершиной треугольника против этой стороны. В нашем примере это 50 % компонента В:

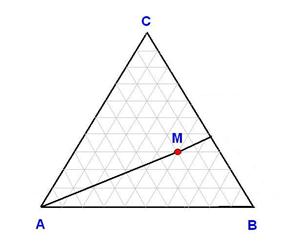
2) Линии, проведенные из вершины треугольника до пересечения с противолежащей стороной, являются геометрическими местами точек, соответствующих ряду систем, в которых соотношение между содержанием двух компонентов остается постоянным (в нашем примере С/В=3:2).

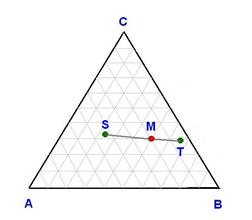
3) К треугольной диаграмме, так же, как и к диаграмме бинарных систем, приложимо правило рычага. Если фигуративная точка М отвечает общему составу системы и система распадается на две равновесные фазы, характеризуемые точками S и T, то количество первой фазы (S) относится к количеству второй (T) как длины отрезков МT/MS:

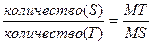
Дата добавления: 2014-01-07