
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Численное интегрирование дифференциальных уравнений в частных производных
|
|
|
|
Преимущества и недостатки КМ
По сравнению с существующими конструкционными материалами КМ обладают рядом преимуществ, среди которых можно выделить:
- сравнительно низкую плотность;
- высокие удельную прочность и удельную жесткость (углепластики, боропластики и органопластики по удельным характеристикам превосходят широко применяемые сплав Д16Т и сталь ЗОХГСА);
- высокие химические и коррозионную стойкость полимерных КМ;
- технологичность переработки КМ в изделия;
- высокие усталостные характеристик волокнистых КМ;
- резкое сокращения количества деталей конструкций агрегатов ЛА;
- специальные свойства (радио прозрачность, диэлектрическая проницаемость, теплопроводность, температуропроводность)
- возможность управления силовыми потоками в конструкциях за счет соответствующего направления армирования.
К недостатка КМ относятся:
- высокая стоимость большинства КМ по сравнению с металлическими сплавами;
- анизотропия физико-механических свойств;
- низкая межслоевая прочность на сдвиг, в плоскостях параллельных арматуре, большинства полимерных КМ;
- низкая прочность большинства полимерных КМ на смятие, затрудняющая соединения деталей крепежными элементами;
- отсутствие зоны текучести, хрупкий характер разрушения, низкая ударная вязкость;
- нелинейный характер физического закона для полимерных КМ при растяжении под углом к направлению армирования;
- невозможность формоизменения заготовок из КМ на термореактивной матрице (штамповкой, обтяжкой);
-необходимость принятия специальных мер по охране труда при переработке КМ в изделия.
Будем рассматривать построение, терминологию и характерные черты метода конечных разностей для уравнений в частных производных на примере неоднородного уравнения теплопроводности
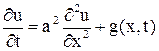 , x Î [0; l ], t Î [0; T], (1)
, x Î [0; l ], t Î [0; T], (1)
сопровождаемого начальным по временной переменной t
u(x, 0) = φ(x) при x Î [0; l ] (2)
и краевыми по пространственной переменной x
u(0, t) = a(t), u(l, t) = b(t) при tÎ [0; T] (3)
условиями.
Как видим, область Ω, на которой определена данная задача, представляет собой прямоугольник (0; l)´(0; T) в системе координат Oxt, а ее граница G состоит из отрезков прямых x = 0, x = l, t = 0 (отрезок прямой t = T здесь к границе Г не относится). Разобьем этот прямоугольник на прямоугольные же части прямыми x = xi и t = tk, параллельными осям Ot и Ox соответственно, где:
xi = ih,  , i = 0, 1,..., n; (4)
, i = 0, 1,..., n; (4)
tk = kt,  , k = 0, 1,..., m. (5)
, k = 0, 1,..., m. (5)
Точки (xi; tk) Î 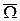 = W È G, лежащие на пересечении этих прямых, называются узлами: внутренними, если они принадлежат области Ω, и граничными, если они лежат на ее границе Г (см. Рис. 1, где внутренние узлы помечены кружочками, а граничные — крестиками; закрашенные кружочки не относятся ни к внутренним, ни к граничным узлам). Совокупность всех узлов в
= W È G, лежащие на пересечении этих прямых, называются узлами: внутренними, если они принадлежат области Ω, и граничными, если они лежат на ее границе Г (см. Рис. 1, где внутренние узлы помечены кружочками, а граничные — крестиками; закрашенные кружочки не относятся ни к внутренним, ни к граничным узлам). Совокупность всех узлов в 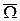 называют сеткой для данной задачи (обозначим ее
называют сеткой для данной задачи (обозначим ее 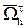 ), а числа h и t, фигурирующие в (4), (5), называют шагами сетки по переменным x и t соответственно. Узлы, лежащие на одной прямой t = tk при фиксированном k = 0, 1,..., m, называют слоем.
), а числа h и t, фигурирующие в (4), (5), называют шагами сетки по переменным x и t соответственно. Узлы, лежащие на одной прямой t = tk при фиксированном k = 0, 1,..., m, называют слоем.
Каждой функции ν(x, t), непрерывной в области 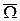 , отвечает единственная таблица ее значений
, отвечает единственная таблица ее значений 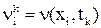 в узлах сетки, называемая сеточной функцией (соответствующей функции n(x, t)). Пометив номер второй координаты узла у сеточной функции верхним индексом, означающим номер слоя, таким же образом будем помечать сеточные функции одной временной переменной:
в узлах сетки, называемая сеточной функцией (соответствующей функции n(x, t)). Пометив номер второй координаты узла у сеточной функции верхним индексом, означающим номер слоя, таким же образом будем помечать сеточные функции одной временной переменной:
ak = a(tk), bk = b(tk), k = 0, 1,..., m. (6)
Разностный метод решения уравнений в частных производных (или, точнее, конечноразностный, поскольку мы используем сетки с постоянным шагом вдоль каждой из осей, что позволяет привлекать конечноразностную интерполяцию) основывается на простой идее построения приближенных сеточных решений: спроектировать данное уравнение на сетку, заменяя входящие в него функции сеточными, а частные производные — их простейшими разностными аппроксимациями. Это проектирование производится следующим образом.
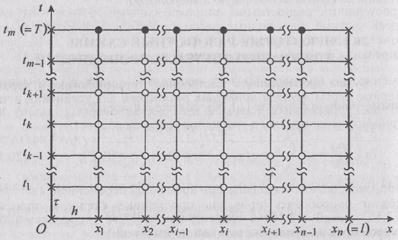
Рис. 1. Сетка  для конечноразностного метода решения задачи (1)-(3).
для конечноразностного метода решения задачи (1)-(3).
Взяв за основу внутренний узел (xi; tk) сетки  , который будем называть расчетным узлом, поставим в соответствие входящей в уравнение (1) функции g(x, t) значение
, который будем называть расчетным узлом, поставим в соответствие входящей в уравнение (1) функции g(x, t) значение  , а частные производные
, а частные производные 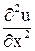 и
и 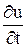 заменим их простейшими разностными аппроксимациями. Ввиду того что здесь частные производные рассматриваются в фиксированной точке, к ним можно применить формулы численного дифференцирования функций одной переменной, изучавшиеся ранее. А именно, для производной
заменим их простейшими разностными аппроксимациями. Ввиду того что здесь частные производные рассматриваются в фиксированной точке, к ним можно применить формулы численного дифференцирования функций одной переменной, изучавшиеся ранее. А именно, для производной 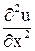 наиболее естественно употребить симметричную формулу (13.20), согласно которой
наиболее естественно употребить симметричную формулу (13.20), согласно которой
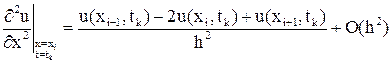 . (7)
. (7)
Для приближенной замены 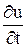 априори с одинаковым успехом можно попробовать привлечь простейшие формулы правой (13.15), левой (13.14) и симметричной (13.18) аппроксимации первой производной; соответственно им имеем:
априори с одинаковым успехом можно попробовать привлечь простейшие формулы правой (13.15), левой (13.14) и симметричной (13.18) аппроксимации первой производной; соответственно им имеем:
 (8)
(8)
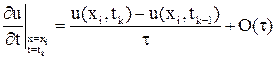 (9)
(9)
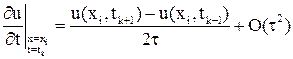 (10)
(10)
Договоримся о следующем.
Во-первых, будем предполагать, что мы находимся в условиях, когда решение u(x, t) данной задачи существует, единственно и обладает достаточной гладкостью.
Во-вторых, в отличие от оговоренных выше обозначений сеточных функций, будем считать, что
 (11)
(11)
т. е. чтобы не вводить другой буквы, через 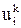 обозначаем значения сеточной функции, соответствующей приближенному решению
обозначаем значения сеточной функции, соответствующей приближенному решению  на сетке
на сетке  , иначе, каркаса приближенного, а не точного решения данной задачи.
, иначе, каркаса приближенного, а не точного решения данной задачи.
Подставив в уравнение (1) аппроксимации 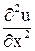 по формуле (7) и
по формуле (7) и 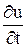 по одной из формул (8), (9) или (10), отбросив погрешности аппроксимаций и учтя при этом обозначение (11), для расчетного узла (xi, tk) получим следующие уравнения:
по одной из формул (8), (9) или (10), отбросив погрешности аппроксимаций и учтя при этом обозначение (11), для расчетного узла (xi, tk) получим следующие уравнения:
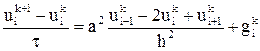 , (12)
, (12)
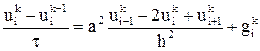 , (13)
, (13)
 . (14)
. (14)
Будем теперь считать, что расчетный узел (xi, tk) смещается по сетке  , т. е. полагаем в уравнениях (12)-(14) i = 1, 2,..., n – 1, k = 1, 2,..., m‑1. Учитывая, что первыми из используемых в расчетах узлами должны быть точки нулевого слоя, а последними — m-го слоя, дополняем множество возможных здесь значений k значением k = 0 для уравнения (12) и значением k = m для уравнения (13).
, т. е. полагаем в уравнениях (12)-(14) i = 1, 2,..., n – 1, k = 1, 2,..., m‑1. Учитывая, что первыми из используемых в расчетах узлами должны быть точки нулевого слоя, а последними — m-го слоя, дополняем множество возможных здесь значений k значением k = 0 для уравнения (12) и значением k = m для уравнения (13).
Сеточные уравнения, которые получаются в результате аппроксимации производных в данном УМФ разностными отношениями, в совокупности с уравнениями, аппроксимирующими на той же сетке начальные и граничные условия (в данном случае, с учетом обозначений (6), это условия
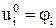 (= φ(xi)), i = 0, 1,..., n, (15)
(= φ(xi)), i = 0, 1,..., n, (15)
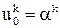 ,
, 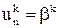 , k = 0, 1,..., m) (16)
, k = 0, 1,..., m) (16)
называются разностными схемами. Конфигурации узлов, в которых связаны одним уравнением разностной схемы значения неизвестной функции — каркаса приближенного решения — называют шаблоном разностной схемы. На Рис. 2 показаны шаблоны, отвечающие разностным схемам (12), (13) и (14) (а, б и в соответственно).
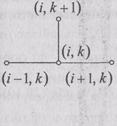


а) б) в)
Рис. 2. Шаблоны для параболического уравнения: а) явный двухслойный; б) неявный двухслойный; в) явный трехслойный
Введем постоянную (при заданной сетке)
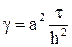 (17)
(17)
и перепишем разностные схемы (12)-(14) соответственно следующим образом:

(где i = 1, 2,..., n – 1; k = 0, 1,..., m – 1); (18)
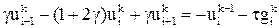
(где i = 1, 2,..., n – 1; k = 1, 2,..., m); (19)
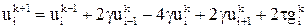
(где i = 1, 2,..., n – 1; k = 1, 2,..., m – 1). (20)
Эти записи позволяют увидеть, как можно осуществить процесс заполнения (n – 1)´m-таблицы значениями 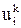 , определяемыми каждой из трех представленных схем.
, определяемыми каждой из трех представленных схем.
Учитывая, что на нулевом слое значения 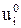 , согласно (15), известны при любом i Î {0, 1, …, n}, формула (18) позволяет непосредственно вычислить все приближенные значения
, согласно (15), известны при любом i Î {0, 1, …, n}, формула (18) позволяет непосредственно вычислить все приближенные значения 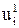 первого слоя. Таким же образом, привлекая найденные значения
первого слоя. Таким же образом, привлекая найденные значения 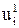 первого слоя, непосредственно можно подсчитать значения
первого слоя, непосредственно можно подсчитать значения 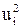 второго слоя, только при этом для вычислений
второго слоя, только при этом для вычислений  и
и  потребуется еще подставить в формулу граничные значения
потребуется еще подставить в формулу граничные значения  и
и  соответственно (см. (16)). Дальнейшие переходы от слоя к слою не отличаются от этого.
соответственно (см. (16)). Дальнейшие переходы от слоя к слою не отличаются от этого.
В равенстве (19) при k = 1 и любом i Î {1, 2, …, n – 1} известна только правая часть благодаря начальным данным (15).
Следовательно, для нахождения значений 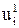 в узлах первого слоя нужно решить СЛАУ
в узлах первого слоя нужно решить СЛАУ
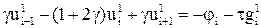 ,
,
где i = 1, 2,..., n – 1;  ,
,  .
.
Очевидно, матрица этой системы имеет трехдиагональную структуру с диагональным преобладанием (1 + 2g > g + g), а это означает, что система может быть эффективно решена методом прогонки. Значения искомой функции и в узлах второго слоя получаются как решение системы

где i = 1, 2,..., n – 1; 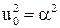 ,
, 
и так далее, т. е. всего для заполнения таблицы требуется решить m однотипных СЛАУ.
Каждая из двух рассмотренных разностных схем связывает значения искомой функции на двух соседних слоях, откуда проистекает их название двухслойные схемы. При этом разностная схема (18), представляющая собой формулу для непосредственного вычисления искомых значений очередного слоя, называется явной схемой, а схема (19), требующая при переходе от слоя к слою решать системы алгебраических уравнений, — неявной схемой.
Исходя из подобного принципа классификации, разностная схема (20) считается явной трехслойной схемой. Правда, поскольку начать процесс вычислений по этой схеме можно только положив k = 1, т.е. с формулы
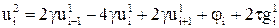 (21)
(21)
где значения 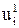 (i = 1, 2,..., n – 1) еще не подсчитаны, нужна дополнительная связь между неизвестными и известными величинами. Такую дополнительную связь между значениями искомой сеточной функции трех первых слоев можно получить, например, беря в качестве расчетного узел нулевого слоя и применяя к
(i = 1, 2,..., n – 1) еще не подсчитаны, нужна дополнительная связь между неизвестными и известными величинами. Такую дополнительную связь между значениями искомой сеточной функции трех первых слоев можно получить, например, беря в качестве расчетного узел нулевого слоя и применяя к 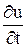 формулу несимметричной аппроксимации второго порядка точности. Имеем
формулу несимметричной аппроксимации второго порядка точности. Имеем
 ,
,
откуда вытекает другое равенство того же вида, что и (21):
 .
.
Сравнением правых частей последнего равенства и равенства (21) приходим к трехточечному разностному уравнению второго порядка
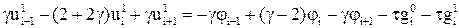 ,
,
решая которое методом прогонки, находим значения функции и в узлах первого слоя, после чего становится возможным счет по формуле (21) и все последующие вычисления по общей формуле (20) при k = 2, 3,..., m – 1.
Аппроксимация, устойчивость, сходимость разностных схем для уравнения теплопроводности
Формальная аппроксимация производных в уравнении (1) на заданной сетке  , а также дискретизация начальных (2) и граничных (3) условий в узлах границы Г области Ω, привели к тому, что данную непрерывную бесконечномерную задачу (1)-(3) мы заменили тремя разными конечномерными задачами (18)-(20) с одинаковыми для них дополнительными условиями (15), (16). Встает вопрос: какое отношение имеют решения новых задач к решению исходной задачи? Можно ли быть уверенным в том, что последовательность решений
, а также дискретизация начальных (2) и граничных (3) условий в узлах границы Г области Ω, привели к тому, что данную непрерывную бесконечномерную задачу (1)-(3) мы заменили тремя разными конечномерными задачами (18)-(20) с одинаковыми для них дополнительными условиями (15), (16). Встает вопрос: какое отношение имеют решения новых задач к решению исходной задачи? Можно ли быть уверенным в том, что последовательность решений 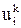 каждого из сеточных уравнений (18)-(20) сходится к значениям решения u(x, t) уравнения (1) на данной сетке
каждого из сеточных уравнений (18)-(20) сходится к значениям решения u(x, t) уравнения (1) на данной сетке  при h ® 0, t ® 0? Ответ на поставленные вопросы обычно дают, опираясь на утверждение о том, что сходимость есть следствие аппроксимации данной бесконечномерной задачи конечномерной и устойчивости решения последней. При этом доказывается, что быстрота сходимости имеет такой же порядок относительно шага (шагов), что и порядок аппроксимации.
при h ® 0, t ® 0? Ответ на поставленные вопросы обычно дают, опираясь на утверждение о том, что сходимость есть следствие аппроксимации данной бесконечномерной задачи конечномерной и устойчивости решения последней. При этом доказывается, что быстрота сходимости имеет такой же порядок относительно шага (шагов), что и порядок аппроксимации.
Установление факта и порядка аппроксимации уравнения (1), а точнее, задачи (1)-(3), рассмотренными выше разностными схемами в предположении о достаточной гладкости решения u(x, t) не вызывает затруднений. Сравнение этих схем в виде (12)-(14) с конечномерными уравнениями, которые получаются в результате подстановки точных равенств (7)-(10) в исходное уравнение (1), показывает, что явная и неявная двухслойные разностные схемы (18) и (19) аппроксимируют уравнение (1) с погрешностью Ο(τ) + + Ο(h2), a явная трехслойная схема (20) — с погрешностью Ο(τ2) + Ο(h2). Так как при проектировании краевых и начальных условий данной задачи на сетку 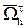 искажений (зависящих от h и от t) не вносится, то можно считать, что с такими же погрешностями эта задача в целом аппроксимируется соответствующими дискретными задачами вместе с условиями (15)-(16). Как правило, о рассмотренных двухслойных схемах, основанных на четырехточечных шаблонах (см. рис. 20.2, а и б), говорят, что они аппроксимируют данную параболическую задачу (1)-(3) со вторым порядком по пространственной переменной x и с первым по временной переменной t, и отражают этот факт записью погрешности аппроксимации задачи вида O(h2 + t). Для трехслойной схемы (20) погрешность аппроксимации составляет величину O(h2 + t2).
искажений (зависящих от h и от t) не вносится, то можно считать, что с такими же погрешностями эта задача в целом аппроксимируется соответствующими дискретными задачами вместе с условиями (15)-(16). Как правило, о рассмотренных двухслойных схемах, основанных на четырехточечных шаблонах (см. рис. 20.2, а и б), говорят, что они аппроксимируют данную параболическую задачу (1)-(3) со вторым порядком по пространственной переменной x и с первым по временной переменной t, и отражают этот факт записью погрешности аппроксимации задачи вида O(h2 + t). Для трехслойной схемы (20) погрешность аппроксимации составляет величину O(h2 + t2).
Несомненно, погрешность аппроксимации данной задачи с помощью каждой из трех рассматриваемых разностных схем (в другой терминологии, локальная ошибка дискретизации) стремится к нулю при h ® 0, t ® 0. Это называется условием согласованности разностной схемы и является лишь необходимым условием стремления к нулю глобальной ошибки, которая может накапливаться по тому или иному закону от слоя к слою. Способность разностной схемы (естественно, при условии ее однозначной разрешимости) не допускать неограниченного увеличения ошибки в процессе измельчения сетки, грубо говоря, и означает ее устойчивость. Поскольку источником первоначальной ошибки может служить переход к сеточным функциям при дискретизации исходного уравнения, а также неточности в начальных и граничных условиях, изучение устойчивости разностной схемы в целом разбивают, соответственно, на изучение устойчивости по правой части, по начальным данным и по граничным условиям.
Исследование устойчивости разностных схем (в смысле той или иной строгой формулировки, которых имеется несколько, но все они базируются на одном и том же понятии устойчивости) является наиболее сложным этапом построения конечноразностного метода. Существует ряд приемов проведения таких исследований: с помощью разностного принципа максимума, с помощью «индекса разностной схемы», методом разделения переменных, изучением роста единичной ошибки и др.
Обратимся к последней разностной схеме (20). К ней целесообразно применить так называемую ε-схему изучения роста единичной ошибки. Суть ее в том, что по исследуемой разностной схеме проводят пробные расчеты, исходя из предположения о единственной ошибке ε в значении 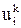 , т. е. вместо этого значения в расчетную формулу подставляют значение
, т. е. вместо этого значения в расчетную формулу подставляют значение  и следят за поведением ошибки на следующих (k + 1)-м, (k + 2)-м,... слоях. Если ошибка имеет тенденцию расти по модулю, то разностная схема должна быть признана неустойчивой и забракована. Такой ε-анализ трехслойной схемы (20) в частном случае γ = 0,5, g = 0 показывает, что начав процесс вычислений с k-го слоя с одним искаженным значением
и следят за поведением ошибки на следующих (k + 1)-м, (k + 2)-м,... слоях. Если ошибка имеет тенденцию расти по модулю, то разностная схема должна быть признана неустойчивой и забракована. Такой ε-анализ трехслойной схемы (20) в частном случае γ = 0,5, g = 0 показывает, что начав процесс вычислений с k-го слоя с одним искаженным значением  , на следующем слое получим значение
, на следующем слое получим значение 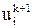 с ошибкой –2ε, далее значение
с ошибкой –2ε, далее значение 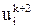 будет иметь ошибку 7ε,..., значение
будет иметь ошибку 7ε,..., значение 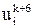 ошибку 1311ε. Ошибка катастрофически растет, что говорит о непригодности разностной схемы (20), по меньшей мере, при g = 0,5, хотя она имеет более высокий порядок аппроксимации по сравнению с двумя другими схемами.
ошибку 1311ε. Ошибка катастрофически растет, что говорит о непригодности разностной схемы (20), по меньшей мере, при g = 0,5, хотя она имеет более высокий порядок аппроксимации по сравнению с двумя другими схемами.
Исследования явной двухслойной схемы (18) приводят к одному: она устойчива при условии g £ 0,5, что в соответствии с обозначением (17) равносильно требованию к шагу по времени
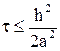 . (22)
. (22)
Разностная схема, устойчивость которой связана с некоторым ограничением на шаг, называется условно устойчивой.
В отличие от явной, неявная двухслойная схема (19) устойчива при любых γ > 0, т.е. при любом соотношении шагов по времени и по пространственной переменной, в связи с чем ее называют безусловно или абсолютно устойчивой разностной схемой.
Таким образом, можно констатировать сходимость решений двухслойных разностных схем (18), (19) с совокупностью дополнительных условий (15)-(16) к решению задачи теплопроводности (1)-(3) с погрешностью O(h2 + t) при любых h ® 0, t ® 0 в случае неявной схемы и при h ® 0, 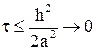 в случае явной схемы. Очевидно, каждая из этих схем имеет свои достоинства и недостатки. Явная схема проще и требует меньше вычислительных затрат на подсчет значений одного слоя, зато таких слоев должно быть больше из-за ограничения (22) на шаг по времени, чем при реализации неявной схемы, допускающей любое соотношение шагов, но требующей решения СЛАУ при подсчете значений каждого слоя. Правда, при этом сопоставлении не следует забывать еще о точности аппроксимации данной задачи разностной схемой, которая для явной схемы (18) при ограничении (22) теперь есть O(h2), и чтобы иметь такую же для неявной схемы, нужно в ней брать τ = O(h2).
в случае явной схемы. Очевидно, каждая из этих схем имеет свои достоинства и недостатки. Явная схема проще и требует меньше вычислительных затрат на подсчет значений одного слоя, зато таких слоев должно быть больше из-за ограничения (22) на шаг по времени, чем при реализации неявной схемы, допускающей любое соотношение шагов, но требующей решения СЛАУ при подсчете значений каждого слоя. Правда, при этом сопоставлении не следует забывать еще о точности аппроксимации данной задачи разностной схемой, которая для явной схемы (18) при ограничении (22) теперь есть O(h2), и чтобы иметь такую же для неявной схемы, нужно в ней брать τ = O(h2).
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1232; Нарушение авторских прав?; Мы поможем в написании вашей работы!