
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выражения единичных векторов
|
|
|
|
| Вектор | Выражение единичного вектора для приведения к системе координат | ||
| статора | ротора | вращающейся со скоростью wк | |
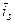
| 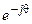
| 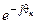
| |

| 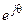
| 
| |

| 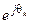
| 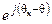
|
Рассмотрим приведение уравнения (14) к системе координат статора. Для этого умножим обе его части на  , а вместо
, а вместо  подставим его значение, выраженное в системе координат статора
подставим его значение, выраженное в системе координат статора 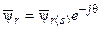 . В результате этого имеем
. В результате этого имеем

или с учётом табл. 1
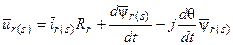
В дальнейшем в уравнения роторной цепи индекс s, указывающий на принадлежность величин к системе координат статора, опускаем. Тогда, представляя выражения w = d q/ dt, окончательно имеем
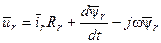 (15)
(15)
Таким образом, уравнения (13) и (15) дают систему дифференциальных уравнений двигателя в векторной форме в системе координат статора.
Аналогичным образом, используя табл. 1 уравнения асинхронной машины можно привести к системе координат, вращающейся с произвольной скоростью wк. В результате преобразований получим:

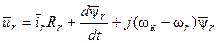 (16)
(16)
где wк = d qк/ dt – угловая скорость вращения системы координат; w r = d q/ dt – угловая скорость вращения ротора.
Векторную запись уравнений можно заменить на скалярную, представив векторы их составляющими по вещественной и мнимой осям (например, для напряжения имеем 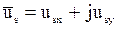 ). В общем случае вещественную ось можно обозначить через х, а мнимую через у. Тогда выражение (16) можно переписать в виде:
). В общем случае вещественную ось можно обозначить через х, а мнимую через у. Тогда выражение (16) можно переписать в виде:
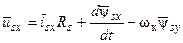
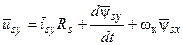 (17)
(17)
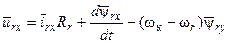
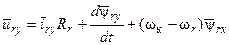
Заменим в системе уравнений (17) величины потокосцеплений на токи согласно выражениям  и
и 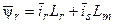 , получим следующую запись дифференциальных уравнений, описывающих поведение машины, где D = d / dt – символ дифференцирования.
, получим следующую запись дифференциальных уравнений, описывающих поведение машины, где D = d / dt – символ дифференцирования.
 (18)
(18)
Уравнения (18) не содержат периодических коэффициентов и образуют систему нелинейных, неоднородных дифференциальных уравнений с постоянными коэффициентами. Нелинейность этих уравнений создаётся произведениями токов и угловой скорости вращения ротора, зависящими от времени.
Теперь выразим результирующий вектор магнитодвижущей силы в составляющих по осям координатной системы. Из (7) получим
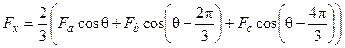
 (19)
(19)
Подставив в (19) значения фазных величин из (4) и сделав преобразования, имеем
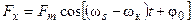
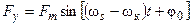 (20)
(20)
Аналогичные преобразования можно выполнить для векторов напряжения и получить

 (21)
(21)
где g0 – значение начального фазового угла напряжения. В симметричной трехфазной системе значения углов g0 и j0 равны нулю.
При исследовании электрических машин нашли применение три координатные системы, которые являются частными случаями рассмотренной системы, вращающейся с произвольной скоростью.
Неподвижная система координат a–b. Результирующий вектор тока, потокосцепления или напряжения можно разложить на составляющие в направлении осей координат, неподвижных в пространстве, т. е. жёстко связанных с осью какой-либо из обмоток статора электрической машины. Эти оси принято обозначать a и b. При этом целесообразно вещественную ось a совместить с направлением оси обмотки, например фазы А. Тогда в любой момент времени вектор тока статора можно определить через его составляющие по вещественной – a и мнимой – b осям, т. е.
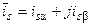 , или
, или 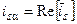 и
и 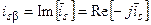 (22)
(22)
Следовательно, магнитное поле, создаваемое током 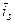 , можно рассматривать как сумму двух полей, создаваемых токами в двух обмотках, расположенных взаимно перпендикулярно в осях a и b. Установим связь между составляющими a, b и мгновенными значениями фазных токов трёхфазной машины. Для составляющей тока по оси a имеем, при условии ia + ib + ic = 0:
, можно рассматривать как сумму двух полей, создаваемых токами в двух обмотках, расположенных взаимно перпендикулярно в осях a и b. Установим связь между составляющими a, b и мгновенными значениями фазных токов трёхфазной машины. Для составляющей тока по оси a имеем, при условии ia + ib + ic = 0:
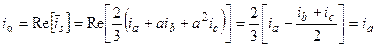
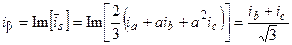 (23)
(23)
Такие же зависимости можно получить для напряжений и потокосцеплений. Дифференциальные уравнения электрической машины в неподвижной системе координат могут быть получены из выражений (17) и (18), если положить wк = 0:
 ;
;  ;
;
 ;
; 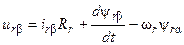 (24)
(24)
или
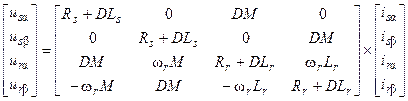 (25)
(25)
Система координат, неподвижная относительно статора, применяется при исследовании машин, имеющих несимметрию электрических цепей статора при симметричной цепи ротора. Она весьма полезна при исследовании электрической машины, получающей питание от статических преобразователей частоты, когда форма напряжения отличается от синусоидальной формы. Достоинство этой системы состоит и в том, что вещественные составляющие векторов (ось a) соответствует реальным физическим значениям величин фазы А, число уравнений и членов в них меньше.
Система координат, неподвижная относительно ротора d–q. Роторы некоторых электрических машин (например, синхронных) обладают магнитной асимметрией, т. е. различными проводимостями в двух взаимно перпендикулярных направлениях в так называемой продольной (d) и поперечной (q) осях. В соответствии с этим полные сопротивления обмоток ротора в продольных и поперечных осях не равны друг другу. Для исследования таких машин целесообразно применить систему координат, неподвижную относительно ротора и вещественную ось которой направить по продольной оси ротора. Вектор тока ротора 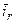 в этой системе и в соответствии с рис. 4 запишется:
в этой системе и в соответствии с рис. 4 запишется:
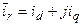 ;
; 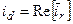 ;
;  (26)
(26)
Здесь также можно магнитное поле ротора представить как сумму двух полей, создаваемых токами id и iq в двух обмотках с взаимно перпендикулярными осями, расположенными на роторе вдоль направлений d и q. Результирующий вектор тока статора также может быть представлен в системе координат ротора. В этом случае составляющие – это токи, обтекающие воображаемую продольную и поперечную обмотки статора, вращающиеся вместе с ротором и создающие такое же магнитное поле, которое образуется действительными токами статора. Зависимость между фазными токами статора и составляющими в направлениях d и q можно вывести на основании табл. 1
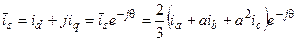

Разложить это выражение на вещественную и мнимую составляющие, получим

 (27)
(27)
По этим составляющим можно определить мгновенные значения фазных токов, проектируя результирующий вектор на оси фазных обмоток
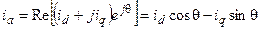
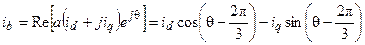 (28)
(28)
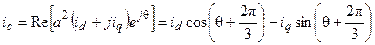
Преобразования координат, осуществляемые по средствам предыдущих формул, называют преобразованием Парка-Горева.
Зависимость между системами координат a–b и d – q можно установить, пользуясь табл. 1
 (29)
(29)
Разложив это уравнение на вещественную и мнимую часть, имеем:

 (30)
(30)
Для обратного преобразования получим
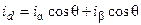
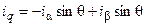 (31)
(31)
Такие же преобразования можно выполнить и для таких величин как напряжение и потокосцепление. Систему дифференциальных уравнений для этой системы можно получить из выражений (17) и (18), положив wк = w r.
Например,
 (32)
(32)
Выражения для напряжений питающих обмотки статора для системы координат d и q можно получить из (21)
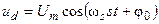
 , (33)
, (33)
где s = (w s – w r) / w s – скольжение.
Если в системе координат, вращающейся со скоростью ротора, обратить внимание на поле статора, то относительно ротора оно окажется неподвижным. Никаких изменений не произойдёт, если ротор остановить, а вращающееся магнитное поле статора заменить неподвижным полем, создаваемое постоянным током. Тогда уравнения будут иметь частоту независимых переменных, равную нулю. Это создаёт определённые преимущества данной системы координат при аналоговом моделировании, где возмущающие воздействия задаются постоянными значениями.
Система координат, вращающаяся с синхронной скоростью. Эта система носит название синхронно вращающихся координат и применяется при исследовании переходных и установившихся режимов в электрических машинах. Система координат неподвижна относительно поля машины в установившемся режиме. Напряжения, являющиеся независимыми переменными, представлены здесь в виде постоянных значений (выражение (21), w s = wк). Это также даёт определённые преимущества при аналоговом моделировании. Недостаток системы заключается в том, что отсутствует решение в виде реальных фазных величин, для получения которых надо выполнить дополнительные преобразования.
Уравнения асинхронного двигателя на основе теории обобщенной машины. Выше выведены уравнения электрической машины переменного тока, определены системы координат, в которых они записываются. В дальнейшем будет рассматриваться определённый тип машины – асинхронный трёхфазный электродвигатель с короткозамкнутым ротором. Выведем уравнения, описывающие поведение такого двигателя через потокосцепления. Учитывая, что  и
и 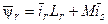 , получим
, получим

 (34)
(34)
Тогда уравнения (16) примут следующий вид:
 ,
,
 , (35)
, (35)
где  ,
, 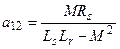 ,
, 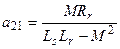 ,
, 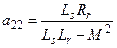 (36)
(36)
Разложив результирующие векторы на составляющие системы координат a–b, будем иметь:
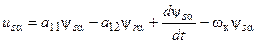
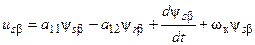
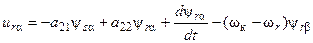
 (37)
(37)
Важными параметрами электрической машины являются электрическая мощность и электромагнитный момент. Напомним, что вращающий момент в электрической машине возникает от воздействия тока, протекающего по проводникам с магнитным потоком машины. Поэтому для определения электромагнитного момента воспользуемся их векторным произведением, и получим
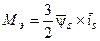
 (38)
(38)
Выразим вектора величин через их составляющие, что дает следующее выражение
 (39)
(39)
Теперь введём понятие единичных векторов по осям: единичный вектор в направлении оси a обозначим через 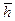 , в направлении оси b –
, в направлении оси b – 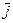 ,а в направлении, перпендикулярном плоскости, в которой расположена система координат α–β, –
,а в направлении, перпендикулярном плоскости, в которой расположена система координат α–β, –  . Тогда применив известное правило умножения векторных величин выражение для электромагнитного момента (39), можно записать в виде:
. Тогда применив известное правило умножения векторных величин выражение для электромагнитного момента (39), можно записать в виде:
 (40)
(40)
Отсюда абсолютная величина электромагнитного момента выразится:
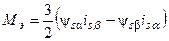 , (41)
, (41)
где 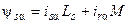 ;
; 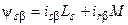 .
.
Если в выражении (38) величину потокосцепления заменить через токи, получим:
 (42)
(42)
Используя предыдущий приём преобразований, будем иметь:
 (43)
(43)
А теперь, если в выражении (38) заменить ток через потокосцепление и сделать преобразования, выражение электромагнитного момента примет вид
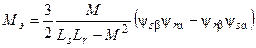 (44)
(44)
Таким образом, для вычисления электромагнитного момента получено три выражения, а, если записать (38) в тех же величинах, относящихся к ротору, то можно получить ещё три выражения для электромагнитного момента. Используя различные преобразования можно получить выражения электромагнитного момента, в которых участвуют сочетания величин тока статора и потокосцепления ротора или наоборот. Наличие нескольких выражений для определения электромагнитного момента является преимуществом, которое реализовывается при математическом моделировании частотноуправляемого электропривода. Например, если выбирается аналоговое моделирование процессов, то целесообразно дифференциальные уравнения записывать в потокосцеплениях, а вычисление момента, проводить по (44). Это объясняется тем, что потокосцепление с точки зрения физических процессов является величиной, мгновенные значения которой не имеют значительных изменений (колебаний) и технически перемножение их аналоговыми методами не предоставляет больших трудностей в смысле получения необходимого результата.
Здесь необходимо особо отметить, что все выводы проводились для двухполюсной трёхфазной машины. В тех случаях, когда необходимо сделать расчёты для m –фазной и р –полюсной машины, это следует учесть определённым способом. Например, выражение электромагнитного момента (38) запишется так:
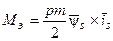 .
.
В дальнейшем общие выводы будут делаться для двухполюсной трёхфазной машины (p = 1, m = 3), а в случае необходимости будет проводиться учёт полюсности и фазности машины.
Приводимые в теории электропривода выражения момента и уравнения механической характеристики приближённые. Наиболее точное из известных выражение электромагнитного момента трёхфазного двигателя имеет вид
 , (45)
, (45)
где m – число фаз, U ф – эффективное значение фазного напряжения, Rs, xs – активное и индуктивное сопротивления фазы статора, R ′ r, x ′ r – приведенные к статору активное и индуктивное сопротивления фазы ротора, ws – угловая скорость электромагнитного поля, р – число пар полюсов, s = 1 – w r / w s – скольжение, с 1 – параметр, значение которого определяется по формуле с 1 = 1 + Zs / Z m. Полные сопротивления статора Zs и контура намагничивания Z m – комплексные величины, что затрудняет вычисления электромагнитного момента по формуле (45). Однако при питании двигателя от сети с промышленной частотой значения Zs и Z m незначительно отличаются от соответствующих реактивных сопротивлений хs и х m. Но при частотном управлении такая замена приводит к погрешности, которая увеличивается при снижении частоты питающего напряжения. Для избежания таких неточностей воспользуемся выражениями, полученными на основании теории обобщённой машины, и выведем уравнения для механической характеристики, электромагнитного момента и мощности. Рассмотрим установившийся режим работы двигателя, для которого уравнения (35) запишутся так, при wк = ws:
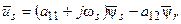
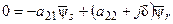 , (46)
, (46)
где d = w s – w r – параметр абсолютного скольжения.
Определитель этой системы уравнений имеет вид:
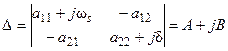 . (47)
. (47)
Здесь A = b – w s d; B = a 22 w s + a 11 d; b = a 11 a 22 – a 12 a 21
Определители при неизвестных имеют следующие выражения:
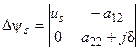 ,
,  (48)
(48)
Тогда решение системы уравнений (46) запишется

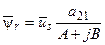 (49)
(49)
Определим проекции результирующих векторов потокосцеплений статора и ротора 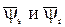 на оси a и b:
на оси a и b:
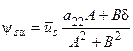 ,
, 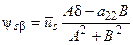 ,
,
 ,
,  . (50)
. (50)
Модули этих векторов можно вычислить по следующим выражениям:
 ,
,  . (51)
. (51)
Воспользуемся для вычисления электромагнитного момента асинхронного двигателя выражением по (43) и получим:
 (52)
(52)
Из условия dM э / d d = 0 найдётся значение критического скольжения dк, при котором двигатель развивает максимальный момент:
 (53)
(53)
Вычислим выражение А 2 + В 2, которое с учётом (2.20) равно:
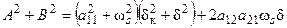
и подставим в (52). Тогда выражение электромагнитного момента примет следующий вид:
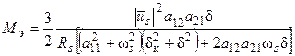 (54)
(54)
Выражение (54) при w r = 0 даёт значение пускового момента, одну из важнейших эксплуатационных характеристик электромашины:
 (55)
(55)
А значение максимального момента определится из (54) при d = dк:
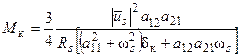 (56)
(56)
Если теперь взять отношение текущего значения момента к его максимальному значению, то можно получить выражение, по форме совпадающее с известным уравнением Клосса:
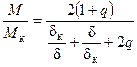 , (57)
, (57)
где 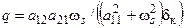 .
.
Выражение (57) можно рассматривать как уравнение механической характеристики двигателя. Вследствие более точного определения параметров М к, dк и q оно может применяться при достаточно малых значениях частоты. При отсутствии нулевых составляющих токов или напряжений мгновенное значение мощности может быть вычислено с помощью выражения пространственных векторов тока и напряжения в соответствии с соотношением:
 (58)
(58)
которое представляет собой скалярное произведение вектора напряжения и вектора тока 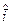 , сопряжённого с вектором
, сопряжённого с вектором  . Это выражение определяет мгновенное значение мощности при любом законе изменения векторов напряжения и тока в зависимости от времени. Выведем сначала выражение для вектора тока статора через параметры электрической машины. Для этого в выражение (34), определяемое ток статора подставим значение соответствующих потокосцеплений из (49) и будем иметь:
. Это выражение определяет мгновенное значение мощности при любом законе изменения векторов напряжения и тока в зависимости от времени. Выведем сначала выражение для вектора тока статора через параметры электрической машины. Для этого в выражение (34), определяемое ток статора подставим значение соответствующих потокосцеплений из (49) и будем иметь:
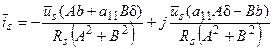 (59)
(59)
Аналогичным приемом получается выражение вектора тока ротора:
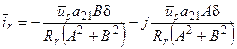 (60)
(60)
Тогда значение мощности, потребляемой из сети, выразится
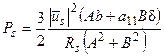 (61)
(61)
Электромагнитному моменту двигателя по (52) соответствует электромагнитная мощность равная:
 (62)
(62)
Полная механическая мощность, развиваемая двигателем на роторе, определится соотношением
 (63)
(63)
Кроме этого, целесообразно иметь уравнение электромагнитного момента, выраженного через потокосцепление статора. Для этого в (52) подставим значение напряжения статора из (51) и получим
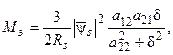 (64)
(64)
Полученные выражения основных величин асинхронного двигателя справедливы как при номинальных параметрах, так и при их изменении и регулировании. В дальнейшем эти выражения будут использованы для анализа зависимостей и вывода законов частотного управления.
Эквивалентная схема асинхронной машины и методика определения её параметров. Известно, что анализ свойств асинхронной машины удобно проводить на основе её эквивалентной схемы, представляющую систему не электромагнитно связанных, а электрически взаимодействующих контуров. Одной из наиболее точных схем замещения является Т-образная схема. Для машины, описывающейся уравнениями, составленными на основе теории обобщённой машины, также можно получить эквивалентную схему, используя дифференциальные уравнения в векторной форме (46) с учётом того, что  и
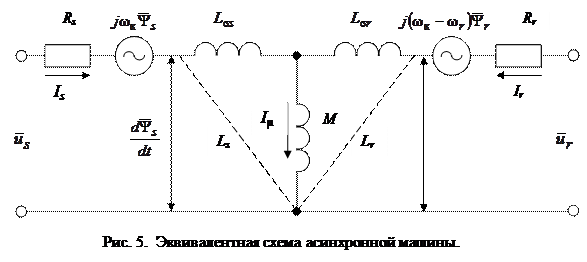
и 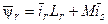 . Она изображена на рис. 5. Как видно предполагаемая эквивалентная схема по структуре аналогична классической. Отличие состоит в том, что в неё введены угловые скорости координатной системы, в которой проведены преобразования цепей статора и ротора. Все полученные ранее выражения характеризующие работу асинхронной машины, а также её эквивалентная схема, имеют в своём составе параметры машины: активные сопротивления, индуктивности обмоток, параметры контура намагничивания и т. д. Для анализа статических и динамических режимов её работы необходимо знать эти параметры. Существуют экспериментальные и расчётные методы их определения. Наибольший интерес представляют методы, основанные на использовании каталожных данных на электрическую машину. Рассмотрим один из них, разработанный на основе ранее изложенных выражений для асинхронной машины.
. Она изображена на рис. 5. Как видно предполагаемая эквивалентная схема по структуре аналогична классической. Отличие состоит в том, что в неё введены угловые скорости координатной системы, в которой проведены преобразования цепей статора и ротора. Все полученные ранее выражения характеризующие работу асинхронной машины, а также её эквивалентная схема, имеют в своём составе параметры машины: активные сопротивления, индуктивности обмоток, параметры контура намагничивания и т. д. Для анализа статических и динамических режимов её работы необходимо знать эти параметры. Существуют экспериментальные и расчётные методы их определения. Наибольший интерес представляют методы, основанные на использовании каталожных данных на электрическую машину. Рассмотрим один из них, разработанный на основе ранее изложенных выражений для асинхронной машины.
Весьма опрометчиво было бы использовать параметры эквивалентной схемы, определённые на основании классической теории асинхронной машины, для упомянутых расчётов, поскольку при обосновании той или иной методики расчёта параметров эквивалентной схемы принимаются различного рода допущения, что влияет на точность вычисления этих параметров. Эти допущения весьма значительны по сравнению с допущениями, использованными в теории обобщённой машины для описания режимов работы асинхронного двигателя. Примером существенного различия допущений является использование Г-образной и Т-образной схемы замещения, последняя из которых более точно описывает асинхронную машину, хотя и она заменила электромагнитносвязанную систему на электрически взаимодействующие контуры. Во избежание влияния различных неточностей и допущений на точность определения параметров схемы замещения было бы рационально разработать методику их определения на основе теории обобщения.
Рассмотрим векторную диаграмму асинхронной машины, соответствующую уравнению для статорной цепи в установившемся режиме, т. е. 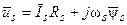 (рис. 6). При этом вектор напряжения статора располагается вдоль оси a системы координат a–b, и его проекция на ось b оказывается равной нулю, а на ось a – значению модуля этого вектора
(рис. 6). При этом вектор напряжения статора располагается вдоль оси a системы координат a–b, и его проекция на ось b оказывается равной нулю, а на ось a – значению модуля этого вектора  .
.

Проведём разложение вектора напряжения на составляющие:
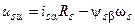
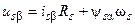
Принимая во внимание эти выражения и используя векторную диаграмму, для точки номинального режима можно найти составляющие потокосцепления статора и его модуль:
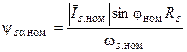 ;
; 
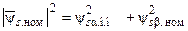 (65)
(65)
Все расчёты проводятся для номинальной точки и поэтому индекс, обозначающий принадлежность к номинальному значению опускается при рассмотрении этого вопроса. Для рассматриваемого расположения векторов напряжения статора в системе координат система уравнений (35) может быть представлена так:
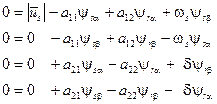 (66)
(66)
Определим значения составляющих потокосцепления ротора по осям системы координат, решая два последних уравнения системы (66)
 , (67)
, (67)
Подставим полученное решение в два первых уравнения системы (66) и получим:
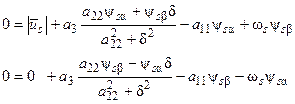 , (67)
, (67)
где а 3 = а 12 а 21.
Решим систему (67) относительно а 11 и а 3 и будем иметь:
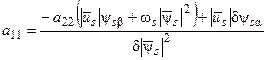 , (68)
, (68)
 (69)
(69)
Используя выражение (52), можно получить следующие коэффициенты:
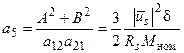 , или а 3 а 5 = А 2 + В 2 (70)
, или а 3 а 5 = А 2 + В 2 (70)
С другой стороны, зная составляющие коэффициентов А и В, можно получить:
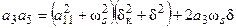 (71)
(71)
Теперь воспользуемся выражением (56) для получения таких коэффициентов как,
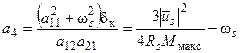 , или
, или 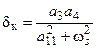 (72)
(72)
Подставим в (71) значение (72):
 (73)
(73)
Из выражения (73) определится:
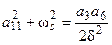 , (74)
, (74)
где  .
.
Теперь, решая совместно уравнения (69), (70) и (74) относительно а 22 получим:
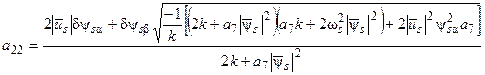 , (75)
, (75)
где 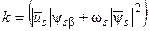 ,
, 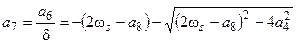 ,
, 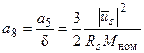
Определив значение коэффициента а 22, проводим вычисление коэффициентов а 11 по (69) и а 3 по (70). А на основании полученных коэффициентов а 11, а 22 и а 3 можно определить другие параметры эквивалентной схемы по следующим выражениям:
 ,
, 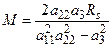 ,
,  ,
, 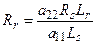 . (75)
. (75)
В корректности значений, полученных параметров эквивалентной схемы можно убедиться утешительной проверкой значений номинального и максимального моментов и сравнений их значения с паспортными данными. Для проведения этих расчётов необходимо вычислить такие коэффициенты как а 12 и а 21 по следующим выражениям:
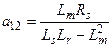 ,
,  ,
,
а значение параметра абсолютного критического скольжения по формуле:

Из анализа изложенного материала можно сделать следующие выводы:
– полученные выражения органически объединяются в общий математический аппарат рассмотрения установившихся и переходных режимов работы машины переменного тока;
– предлагаемая методика вычисления параметров эквивалентной схемы асинхронного двигателя основана при меньшем количестве допущений, что повышает точность их определения, а их использование для расчетов в «домашней» системе уравнений режимов статики и динамики, следовательно, также положительно скажется на результатах вычислений;
– при вычислении параметров эквивалентной схемы определяются его индуктивности, а не индуктивные сопротивления, что позволяет избежать учёта высших гармонических в расчётах статики и динамики регулируемого электропривода, особенно при частотном управлении машин переменного тока;
– предлагаемые выражения, как для расчёта законов частотного управления, так и по определению параметров достаточно легко решаются средствами современной микропроцессорной техники. Поэтому предлагаемая методика может быть заложена в систему управления преобразователем с целью управления асинхронной машиной в реальном масштабе времени, т. е. управления, реализующего учёт изменения её параметров на законы параметрического или частотного управления в процессе их реализации;
– предлагаемый математический аппарат рационален для создания обобщённых виртуальных моделей частотно-регулируемого электропривода в вычислительной среде Matlab-Simulink.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 914; Нарушение авторских прав?; Мы поможем в написании вашей работы!