Лекция 23 Основы зонной теории кристаллов

1. Кристаллическая структура; типы связей в кристаллах

2. Колебания решетки. Фононы

3. Основные представления зонной теории; энергия Ферми

Твёрдыми телами называют тела, для которых характерно постоянство формы и объема при неизменных физических условиях. Твёрдое состояние вещества реализуется при настолько сильном взаимодействии между молекулами (атомами, ионами), что энергия связи молекул значительно превышает энергию их теплового движения.

Различают кристаллические и аморфные твердые тела.

Кристаллы (в греческом языке «krystallos» означает лёд) – твердые тела, обладающие трехмерной периодической атомной структурой и – при образовании в равновесных условиях – имеющие естественную форму правильных симметричных многогранников.

Кристаллы ограничены плоскими, упорядоченно расположенными друг относительно друга гранями, сходящимися в рёбрах и вершинах. Внешние грани кристалла образуют друг с другом постоянные углы, величина которых зависит от типа симметрии в расположении атомов в кристалле. Как следствие – монокристаллы разных веществ отличаются по внешнему виду, или габитусу, и часто кристаллическое вещество можно идентифицировать по внешнему виду его отдельного кристалла.

При температурах ниже точки кристаллизации кристаллическое состояние является устойчивым состоянием всех кристаллических тел. Точки равновесного положения составляющих кристалл атомов, молекул или ионов называют узлами кристаллической решётки.

Большинство кристаллических твердых тел является поликристаллами – для таких тел характерна мелкокристаллическая структура, они состоят из большого числа сросшихся мелких, хаотически расположенных кристаллов (кристаллических зёрен, кристаллитов).

Для кристаллических веществ характерно большое число вариаций их физических свойств, обусловленных симметрией строения и анизотропией кристаллов. До начала ХХ века область использования монокристаллов ограничивалась почти исключительно ювелирной промышленностью. С начала 20-х годов ХХ века возникла потребность в массовом производстве качественных, бездефектных монокристаллов в целях их применения в науке и технике – как отрасль промышленности возникло выращивание кристаллов с заданными свойствами. На использовании своеобразных свойств кристаллов базируются и развиваются новые отрасли науки и техники.

По характеру сил взаимодействия, типу связи и в зависимости от того, какие частицы расположены в узлах кристаллической решётки, различают кристаллы следующих типов:

– металлы (натрий, железо и др.). При сближении атомов, находящихся в начале каждого периода системы элементов Д.И. Менделеева, валентные электроны покидают свои атомы и мигрируют по кристаллу, образуя электронный газ в металле. Эти электроны называют электронами проводимости. Отделение электронов от внешних оболочек атомов, несмотря на необходимость энергетических затрат, влечет за собой уменьшение энергии всего металла, что подтверждается самим фактом существования электронов проводимости в металле. Только вблизи узлов кристаллической решетки (концентрация атомов в металлах ~10²⁸ м^-3) плотность электронов увеличивается, что обусловлено электронами внутренних оболочек атомов.

Так как взаимодействие коллективизированных электронов преимущественно электростатическое, они удерживают в кристаллической структуре положительно заряженные ионы – силы притяжения при определённом периоде решетки уравновешивают силы электростатического отталкивания ионов, и возникает устойчивая металлическая решетка кристалла – структурные элементы металла удерживаются в положениях равновесия (в узлах кристаллической решётки). Возникающую при этом связь между атомами металла называют металлической связью. Потенциальная энергия взаимодействия металлической связи составляет сотни кДж/моль (например, 110 кДж/моль у натрия и 390 кДж/моль у железа).

Металлы отличаются высокой теплопроводностью и электрической проводимостью, специфическим металлическим блеском, особыми механическими свойствами, в силу которых они поддаются ковке и штамповке;

– ионные кристаллы (хлористый натрий, фторид лития, оксиды металлов, сульфиды, карбиды, селениды и др.) характеризуются ионной (гетерополярной) связью между правильно чередующимися в узлах кристаллической решетки положительными и отрицательными ионами. Ионная связь возникает вследствие обмена электроном между атомами, один из которых легко теряет его, превращаясь в положительный ион, а другой приобретает его и превращается в отрицательный ион. Распределение электронов вблизи каждого иона близко к сферически симметричному и слабо нарушается в области соприкосновения соседних ионов. Потенциальная энергия связи составляет ~ 1 MДж/моль (например, у LiF она равна 750 кДж/моль, у NaCl – 764 кДж/моль). Характерными свойствами ионных кристаллов являются: высокая температура плавления, большие значения удельной теплоты сублимации, интенсивные полосы поглощения в инфракрасной области, низкая электрическая проводимость и теплопроводность при низких температурах. При высоких температурах им свойственна значительная ионная проводимость;

– ковалентные (атомные) кристаллы (углерод, кремний, германий, теллур и др.) имеют кристаллическую решетку, характерную для полупроводников и многих органических твердых тел. Кристаллы такого типа образуются из лёгких элементов средних столбцов периодической системы и характерны для некоторых металлов и интерметаллических соединениё. Химическая связь между нейтральными атомами – гомеополярная связь – обусловлена квантовомеханическим обменным взаимодействием и возникает в результате обобществления валентных электронов. Для таких кристаллов типично такое строение решётки, при котором число ближайших атомов, окружающих рассматриваемый атом, равно валентности элемента. Плотность электронного облака обобществлённых электронов между атомами очень быстро изменяется при изменении расстояния между ядрами, поэтому силы взаимодействия при ковалентной связи обычно достаточно велики. Потенциальная энергия связи составляет 700 – 1200 кДж/моль (например, энергия связи у алмаза – типичного ковалентного кристалла – 710 кДж/моль). Основные свойства ковалентных кристаллов – высокая температура плавления и высокая удельная теплота сублимации, высокая механическая прочность (твёрдость), низкая электрическая проводимость чистых образцов при низких температурах, высокие значения показателя преломления;

– молекулярные кристаллы (Ar, CH₄, парафин, почти все органические кристаллы и многие другие твёрдые органические соединения) представляют слабо связанные агрегаты молекул, локализованных в узлах кристаллической решётки, между которыми связь осуществляется посредством сил Ван-дер-Ваальса, в основном дисперсионных. Молекулярная связь – единственно возможный тип связи у кристаллов, образованных из атомов инертных газов. Потенциальная энергия связи составляет ~ 10 кДж/моль (например, у Ar 7,5 кДж/моль, у CH₄ – 10 кДж/моль). Основные свойства молекулярных кристаллов – низкая температура плавления, кипения и возгонки, сильная сжимаемость и плотная упаковка молекул в решётке. Инертные газы, превращаясь в твердое тело, образуют плотноупакованную кубическую структуру;

– кристаллы с водородными связями (лёд, HF и др.). Водородная связь возникает, когда между электроотрицательными атомами (атомами, обладающими большим сродством к электрону[1], например, ) находится атом водорода .

Электрон в атоме водорода слабо связан с протоном, поэтому электронная плотность смещается к атому с более высоким сродством к электрону, а степень экранирования протона атома водорода уменьшается, что способствует сближению электроотрицательных атомов соседних молекул. Водородную связь характеризуется потенциальной энергией ~ 20 кДж/моль. Подобная связь реализуется между молекулами воды. Вместе с притяжением молекул H₂O, обусловленным наличием у них дипольных моментов, водородная связь обеспечивает особые свойства воды и льда при температуре близкой к 4°С. Водородная связь осуществляется между белковыми молекулами, обеспечивая их специфическую геометрию, и имеет большое значение в процессе полимеризации – в образовании групп однотипных молекул.

В реальных ситуациях чаще всего действуют одновременно несколько типов связей, но обычно удается выделить из них ту, которая доминирует.

Между кристаллическим строением твердых тел и их химическим составом существуют связи, исследуемые в кристаллохимии. Всякое химически индивидуальное вещество характеризуется определенными элементами симметрии кристаллов. Важнейшими положениями кристаллохимии являются:

– сходство формы кристаллов у веществ с аналогичным химическим строением (изоморфизм);

– возможность существования нескольких кристаллических форм для твёрдых тел одного химического состава, каждая из которых устойчива в различных условиях (полиморфизм).

В развитии кристаллохимии и всего учения о кристаллических твердых телах большое значение имеет рентгеноструктурный анализ. На его основе установлено, что каждый структурный элемент кристалла (атом, ион) имеет практически непроницаемую «сферу действия» и расстояния между атомами в кристаллах являются суммами радиусов их сфер действия. Так, структура ионных кристаллов существенно зависит от соотношения ионных радиусов.

Вследствие закономерности и симметрии структуры кристаллов они однородны и анизотропны. Так как расстояния и силы связи между частицами в различных направлениях в кристалле неодинаковы, то большинство свойств кристалла анизотропно, но эти свойства одинаковы в направлениях, симметричных друг другу. Например, слюда легко расщепляется по плоскостям спайности, а вдоль других плоскостей расщепить её не удается. Анизотропия свойств проявляется и при росте кристаллов – в различных направлениях скорость роста кристалла неодинакова; это проявляется во внешней форме кристалла. Подробное описание свойств кристаллов с учетом их симметрии можно найти в учебных пособиях и научной литературе по кристаллофизике и кристаллохимии, а описание свойств симметрии и классификацию кристаллов на основе элементов симметрии – в курсах кристаллографии.

Один из основных видов внутренних движений твёрдого тела – колебания его кристаллической решётки. Составляющие твёрдое тело частицы (атомы, ионы, молекулы) совершают колебания около положения равновесия – узлов кристаллической решётки. Амплитуда колебаний тем больше, чем выше температура, но всегда существенно меньше постоянной решётки. Если амплитуда колебаний превышает некоторое критическое значение, кристаллическая структура разрушается – начинается плавление кристаллического твёрдого тела. Понижение температуры, наоборот, сопровождается уменьшением амплитуды колебаний, но полного прекращения колебаний не происходит даже при абсолютном нуле температуры. Полное прекращение колебаний при T = 0 K запрещено законами квантовой механики (это противоречило бы соотношениям неопределённости – одновременно точно были бы известны координаты и импульс частиц). При T = 0 K атомы совершают так называемые нулевые колебания, характеризующиеся малой энергией. Поэтому при понижении температуры все жидкости затвердевают. Исключением из них является жидкий гелий, который при T = 0 K затвердевает только при повышенном давлении.

На колебания кристаллической решётки могут налагаться звуковые колебания, обусловленные распространением в кристалле упругих волн, возникающих вследствие внешнего воздействия (однократного удара или воздействия периодической внешней силы).

Под колебаниями атомов и ионов понимают колебания массивных по сравнению с электронами атомных ядер. В таком приближении, называемом адиабатическим, можно считать, что энергия кристалла зависит только от координат ядер.

В результате совместного действия сил притяжения и отталкивания между частицами, а также вследствие отсутствия полной периодичности в расположении частиц в реальном кристалле колебания не являются гармоническими.

Гармоническим (квазиупругим) колебаниям соответствует квадратичная зависимость энергии взаимодействия частиц U(x) от величины смещения x от положения равновесия. Ангармоничность колебаний учитывается посредством введения в выражение для энергии взаимодействия следующих после квадратичного членов разложения в ряд функции U(x) по степеням x:

где U_o – значение U при x = 0, β₀ – коэффициент квазиупругой силы, b – коэффициент ангармоничности.

Тепловое расширение твердого тела связано с ангармоничностью тепловых колебаний частиц его кристаллической решетки. Коэффициент линейного расширения связан с коэффициентом ангармоничности b: , где r₀ – равновесное расстояние между соседними частицами твердого тела.

Передача энергии связанных колебаний узлов решетки в кристаллических диэлектриках имеет основное значение в механизме теплопроводности. В первом приближении этот процесс можно представить в виде распространения в кристалле набора гармонических упругих волн, имеющих различные частоты ν_i. В квантовой теории этим волнам сопоставляются квазичастицы – фононы – с энергиями 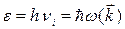и квазиимпульсами , модуль которых , где – скорость упругих волн (скорость звука) в кристалле, 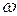– частота колебаний атомов, – квазиволновой вектор.

Колебательная энергия кристалла приблизительно равна сумме энергий фононов. В энергию фононов не принято включать энергию нулевых колебаний решётки. Число тепловых фононов тем больше, чем выше температура кристалла T. Среднее число фононов данного типа, имеющих энергию 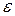, определяется по формуле Планка:

.

Эта формула совпадает с функцией распределения по энергиям частиц газа, подчиняющихся статистике Бозе – Эйншейна, когда химический потенциал [2]. Это означает, что фононы – бозоны.

На основе представлений о фононах как квантах энергии, соответствующих квазиупругим колебаниям узлов кристаллической решетки, удалось определить многие важные физические параметры кристаллов и объяснить механизм физических явлений, в частности, эти представления оказались плодотворными при объяснении теплового расширения твердых тел, их теплопроводности и теплоемкости.

В соответствии с так называемым приближением сильной связи, из соотношения неопределенностей для энергии и времени следует образование зонного энергетического спектра для кристалла. В изолированном атоме, вследствие конечности времени жизни электрона в возбужденном состоянии (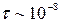с), естественная ширина энергетического уровня 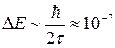эВ. В кристалле валентные электроны атомов, слабее связанные с ядром, чем внутренние электроны, могут переходить от одного атома к другому вследствие туннельного эффекта – просачивания сквозь потенциальный барьер, разделяющий атомы в кристалле. Этим обусловлено то, что существенно уменьшается, и энергетические уровни таких коллективизированных электронов расширяются в зоны (полосы) разрешенных значений энергии.

При увеличении энергии электрона ширина разрешенных зон увеличивается. Это связано с тем, что с увеличением энергии электронам легче проникать через потенциальные барьеры, и наличие потенциальных барьеров всё меньше сказывается на движении электронов. При 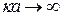электрон ведет себя как свободный.

Частота просачивания электрона сквозь барьер прямоугольной формы равна

,

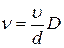где – скорость электрона в атоме, – линейный размер атома, – прозрачность барьера. Принимая в соотношении неопределенностей среднее время жизни электрона у данного атома 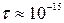с, получим оценочное значение неопределённости энергии 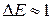эВ. Таким образом, в кристалле вместо узкого энергетического уровня 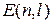валентного электрона изолированного атома образуется зона разрешенных значений энергии шириной эВ.

Вероятности туннельных переходов в кристалле для электронов внутренних оболочек атомов ничтожно малы. Эти электроны остаются в кристалле прочно связанными со своими атомами, и их энергетические уровни – столь же узкими, как и в изолированном атоме.

Физически происхождение зонной структуры энергетического спектра электронов в кристалле связано с образованием кристалла из многих атомов, каждый из которых в свободном состоянии обладает дискретным электронным энергетическим спектром. При объединении атомов в кристалл последний можно трактовать как гигантскую молекулу, в которой электроны всех атомов обобществлены и которую следует рассматривать как единую квантово-механическую систему. Общее число энергетических уровней электронов в пределах зоны конечно и для кристалла, состоящего из 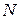одинаковых атомов, равно 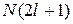, где – орбитальное квантовое число электрона, находящегося на исходном энергетическом уровне в изолированном атоме. В соответствии с принципом Паули, на каждом таком уровне может находиться не более двух электронов, отличающихся ориентацией спина. Соответственно, в разрешенной энергетической зоне не может быть больше чем 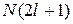коллективизированных электронов.

Таким образом, в кристалле каждый из атомных уровней превращается в полосу, состоящую из N уровней (или, с учетом спина, из 2N уровней), которая является разрешенной зоной. На рисунке 23.1 такое превращение схематически показано для натрия.

Если на атом приходится Z электронов, то полное число электронов в кристалле равно NZ; они занимают уровни разрешенных зон, начиная с нижнего, пока не будут полностью размещены.

Значение энергии, ниже которого все состояния системы частиц, подчиняющихся статистике Ферми – Дирака (фермионов) при абсолютном нуле температуры заняты, называют энергией Ферми. Существование энергии Ферми – следствие принципа Паули, в соответствии с которым в одном квантово-механическом состоянии не может находиться более одного фермиона.

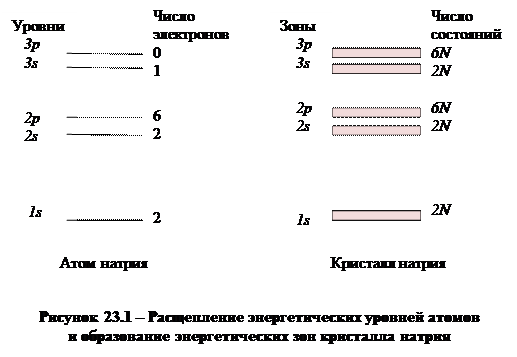Для идеального вырожденного газа фермионов энергия Ферми совпадает со значением химического потенциала при T = 0 К и может быть выражена через число N частиц газа в единице объема:

, (23.1)

где m и S – масса и спиновое квантовое число частицы соответственно. Величина

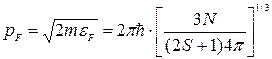(23.2)

называется ферми-импульсом. При T = 0 К все состояния с импульсами 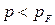заняты, а состояния с свободны. Величина называется ферми-скоростью, или граничной скоростью и определяет верхнюю границу скорости фермионов при T = 0 К.

Изоэнергетическая поверхность, соответствующая энергии Ферми: , называется поверхностью Ферми.

Понятие об энергии Ферми используется в физике твердого тела, в ядерной физике, в астрофизике и т.д. Величина энергии Ферми существенно зависит от физических свойств системы. В металлах обычно 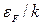~ 10⁵К, в полупроводниках ~ 10² К, в ³He – около 1 К, а в звёздной материи может достигать миллионов кельвин.

Рассмотрим квантово-механическое описание состояний электронов в кристалле. Электроны взаимодействуют между собой и движутся в трехмерном периодическом поле, создаваемом кристаллической решеткой кристалла, в узлах которой находятся неподвижные ядра атомов. Точное решение такой задачи невозможно. Его заменяют решением приближенной задачи (приближение Хартри – Фока) о движении одного электрона в стационарном потенциальном поле 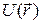атомных ядер и всех остальных электронов. Это поле называют самосогласованным полем.

Основы теории движения электрона в самосогласованном поле кристалла созданы немецким физиком Ф. Блохом (1928 г.) и французским физиком Л. Бриллюэном (1930 г.).

Так как в результате решения соответствующей квантово-механической задачи оказалось, что спектр энергий электрона состоит из чередующихся зон (полос) разрешённых и запрещённых энергий, то описание движения электрона в стационарном потенциальном поле атомных ядер и всех остальных электронов получило название зонной теории твёрдых тел.

В основе зонной теории лежит так называемое одноэлектронное приближение, которое базируется на следующих упрощениях:

1) атомные ядра в узлах идеальной кристаллической решётки неподвижны (их масса велика по сравнению с массой электронов);

2) электрон движется в поле периодического потенциала 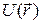, которое является суперпозицией полей, создаваемых ядрами и остальными электронами, и зависит от пространственных координат точки (от радиус-вектора );

3) это периодическое поле обладает трансляционной инвариантностью:

, (23.3)

где – вектор, определяющий положение n -го узла кристаллической решетки.

В такой модели для волновой функции электрона в решётке выполняется теорема Блоха:

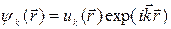, (23.4)

где , – волновой вектор электрона. Это означает, что 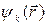имеет вид волновой функции свободного электрона, амплитуда которой модулирована в пространстве и период модуляции равен постоянной решетки. Волновая функция в соседних ячейках отличается фазовым множителем . Поэтому после нахождения в пределах одной ячейки, можно определить волновую функцию для всего кристалла.

Спектр энергии электронов можно определить, подставляя волновую функцию в виде (23.4) в стационарное уравнение Шрёдингера

(23.5)

и учитывая те или иные граничные условия.

Основные свойства решения уравнения Шрёдингера (23.5) при условии (23.4) легко выяснить, рассматривая одномерную модель кристалла Кронига – Пенни (рисунок 23.2) – одномерную последовательность прямоугольных потенциальных барьеров и ям.

Для одномерного периодического потенциала Кронига – Пенни уравнение Шрёдингера имеет вид:

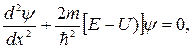(23.6)

где U = 0 в каждой потенциальной яме и U = U₀ – в каждом потенциальном барьере.

Будем искать решение уравнения (23.6) в виде

(23.7)

где – функция, удовлетворяющая условию

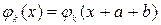. (23.8)

Подставляя (23.7) в (23.6), получим

(23.9)

где

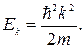(23.10)

В потенциальной яме, где (например, при 0 < x < a) решение уравнения (23.9) имеет вид:

(23.11)

где введено обозначение

(23.12)

В области потенциального барьера (например, в интервале значений a < x < a + b) решение может быть записано в следующем виде:

(23.13)

где

(23.14)

Постоянные А, B, C и D выберем так, чтобы функция φ и её производные 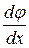были непрерывны на границах областей с различной потенциальной энергией. С учётом этих граничных условий и условия периодичности функции φ получим систему уравнений

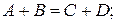
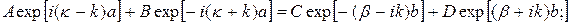
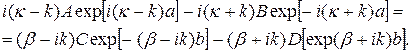(23.15)

Чтобы существовали нетривиальные решения системы уравнений (23.15), детерминант, составленный из коэффициентов, должен быть равен нулю. Если это условие выполнено, то имеет место соотношение

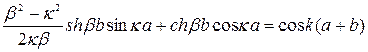, (23.16)

в котором связаны между собой энергия E и значение волнового числа k. Из выражения (23.16) принципиально возможно определить энергию как функцию от k, то есть найти или, наоборот, рассчитать k, соответствующее определённому значению энергии, то есть получить функцию .

Наиболее характерной особенностью соотношения (23.16) является то, что энергия – неоднозначная функция волнового числа k. Для анализа этого обстоятельства целесообразно привести уравнение (23.16) к более удобному виду. Выделим предельный случай, когда ширина потенциального барьера стремится к нулю , а высота его стремится к бесконечности 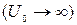– так, чтобы площадь оставалась постоянной. Полагая

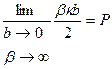(23.17)

и учитывая, что при указанных условиях 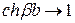, , вместо (23.16) получим уравнение

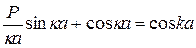. (23.18)

Правая часть выражения (23.18) при вещественных значениях k должна удовлетворять условиям . Следовательно, величина может принимать только такие значения, при которых значения величины не выходят за эти пределы. Это означает, что волновое уравнение имеет решение в виде незатухающих волн только в определенных (разрешённых) энергетических зонах (рисунок 23.3).

Таким образом, при наличии в кристалле N атомов формируется N потенциальных ям, и при конечном значении величины P каждое квантовое состояние выделенного атома (без учёта спина) расщепляется на N квантовых состояний. Иначе говоря, каждый энергетический уровень электрона расщепляется на N подуровней – энергетический уровень отдельного электрона превращается в зону энергетических уровней кристалла (рисунок 23.1). На рисунке 23.3 видно, что при заданном значении P ширина разрешённых энергетических зон увеличивается при возрастании , то есть при возрастании энергии. С ростом P увеличивается ширина любой зоны. Это объясняется тем, что параметр P определяет эффективность потенциальных барьеров, разделяющих области с нулевым потенциалом. При увеличении P «проницаемость» потенциальных барьеров для электронов уменьшается, и при 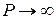электроны оказываются полностью запертыми в потенциальных ямах. При этом ширина энергетических зон стремится к нулю, и разрешёнными оказываются только те решения, для которых значения кратны π, то есть электрон движется в одномерной бесконечно глубокой потенциальной яме и спектр его энергий определяется в соответствии с формулой (7.9):

,

где n = 1, 2, 3, ….

При увеличении энергии электрона параметр в уравнении (23.17) уменьшается, а ширина разрешённых зон энергии увеличивается. Это связано с тем, что электронам с большей энергией легче просочиться через потенциальные барьеры и наличие барьеров по мере увеличения энергии электронов всё меньше влияет на движение электронов. При 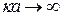электрон ведёт себя как свободный.

Определяемый на основе информации, представленной на рисунке 23.3, спектр разрешённых энергий 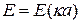может быть пересчитан и представлен в виде зависимости .

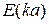Разрешенные энергетические зоны определены в одинаковых по протяженности интервалах 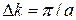. Соответствующий зоне интервал энергий уменьшается с увеличением энергии электронов. Ширина запрещённых зон, наоборот, растёт с увеличением энергии электронов. В области очень больших энергий зависимость приближается к зависимости 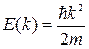для свободных электронов. Однако и при конечных значениях энергии энергетический спектр похож на спектр энергий свободного электрона. В пределах каждой энергетической зоны энергия изменяется непрерывно, что обусловлено предположением о бесконечности цепочки атомов. Вблизи границ зон отличие от спектра свободного электрона становится существенным. Если число атомов в цепочке конечное, то после учёта граничных условий на её концах окажется, что спектр энергий в пределах зоны дискретен. Наличие запрещённых энергетических зон имеет большое значение также в явлениях электропроводности. При рассмотрении вопросов электропроводности твёрдых тел наиболее важны именно энергетические уровни вблизи границ зон, и указанными отличиями нельзя пренебрегать.

Таким образом, уровни энергии электрона в периодическом поле образуют отдельные полосы – зоны разрешенных значений энергии (разрешенные зоны), в каждой из которых энергия зависит от волнового числа 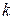(квазинепрерывный энергетический спектр в зоне: 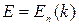, где n = 1, 2, … – номер зоны). Разрешенные зоны отделены друг от друга запрещенными зонами – интервалами запрещенных значений энергии электрона. В пределах каждой разрешенной зоны энергия электрона является четной периодической функцией волнового числа:

.

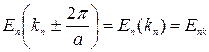Собственная волновая функция оператора энергии электрона, соответствующая собственному значению энергии электрона, имеет вид модулированной плоской волны:

,

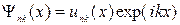где 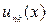– периодическая функция с периодом , конкретное выражение которой зависит от вида функции , характеризующей периодическое поле.

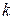На рисунке 23.4 представлена зависимость от волнового числа для первых трёх разрешённых зон. При этом в силу периодичности функции область изменения ограничена пределами от 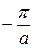до (первая зона Бриллюэна [3] для одномерной решетки).

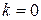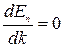На границах разрешенных зон энергии (то есть при и ) . Соответственно, вблизи этих значений 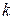зависимость 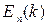можно представить в форме:

(вблизи ),

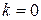(вблизи ),

где и 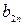– постоянные, а .

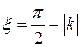Сравнивая эти выражения с энергией электрона, движущегося в изолированной потенциальной яме 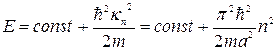, видим, что отличие движения электрона в периодическом поле от его свободного движения можно учесть, заменяя обычную массу 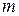эффективной массой :

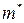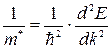. (23.19)

На рисунке 23.4 видно, что у «дна» разрешенной зоны эффективная масса электрона 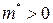, а у «потолка» той же зоны . Поэтому электрон, находящийся вблизи «потолка» разрешенной зоны, движется под действием приложенного к кристаллу электрического поля так, как если бы он имел положительную массу 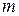и положительный эффективный заряд .

В соответствии с зонной теорией, движение электрона в решетке сходно с движением электрона в свободном пространстве, однако фактически носит туннельный характер. Квазиимпульс электрона в решетке отличен от импульса свободного электрона. Для него выполняются законы сохранения, а также уравнение движения , где – внешняя сила. Электрон в кристалле оказывается квазичастицей с эффективной массой , отличной от массы свободного электрона 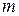, что обусловлено взаимодействием частиц вещества.

Эффективная масса не определяет ни инерционных, ни гравитационных свойств электрона, ни его энергии. Она является только коэффициентом пропорциональности между ускорением электрона, находящегося вблизи границы энергетической зоны, и действующей на него силой. Введение понятия эффективной массы при определённых условиях удобно для описания процессов, происходящих в системе электронов, находящихся в кристаллическом теле, так как при этом удаётся описывать их с применением законов движения свободных электронов. Отличие эффективной массы электрона от массы свободного электрона обусловлено действием на него периодического поля решетки кристалла.

Эффективная масса не только отличается от массы свободной частицы, но и не является постоянной величиной – эффективные массы электронов, находящихся на разных уровнях внутри энергетических зон, в общем случае неодинаковы; с изменением состояния электрона может изменяться и его эффективная масса.

[1] Сродство к электрону – величина, равная разности энергии основного состояния нейтрального атома (молекулы) и энергии основного состояния отрицательного иона, образовавшегося после присоединения электрона. Величиной характеризуется способность некоторых нейтральных атомов, молекул и свободных радикалов присоединять добавочные электроны, превращаясь в отрицательные ионы.

[2] Химический потенциал μ — один из термодинамических параметров системы, а именно энергия добавления одной частицы в систему без совершения работы.

[3] Первая зона Бриллюэна – область обратного пространства с центром в начале координат, определяемая следующим образом: если построить плоскости, проходящие через середины векторов, соединяющих начало координат с ближайшими узлами обратной решетки, то образованный ими многогранник и есть первая зона Бриллюэна. Первая зона Бриллюэна обладает теми свойствами симметрии относительно операций поворота, зеркального отражения и инверсии, что и решетка Браве данного кристалла, характеризующая возможные типы трансляционной симметрии кристаллической решетки. Объем обратного пространства, заключенный в первой зоне Бриллюэна, равен, где – объем элементарной ячейки для решетки Браве.

Дата добавления: 2014-01-07