
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференцируемость функции в точке и на промежутке
|
|
|
|
Производная функции, согласно ее математического определения (5) и (6) – это некий предел. Но, как и всякий предел, он может оказаться:
а) конечным; б) бесконечным; в) вообще не существовать.
Если для данного x имеет место вариант (а), то есть если при заданном x производная 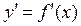 функции
функции 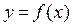 существует и конечна, то эта функция называется дифференцируемой в точке x.
существует и конечна, то эта функция называется дифференцируемой в точке x.
Функция, дифференцируемая в каждой точке x некоторого промежутка оси ох (например, интервала (a; b) или отрезка [ a; b ]) называется дифференцируемой на этом промежутке. Кстати, сама процедура вычисления производной функции называется ее дифференцированием (продифференцировать функцию – это значит найти ее производную).
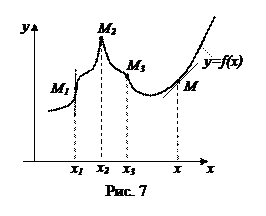 Из геометрического смысла производной функции, определяемого равенством (11) и рис.5, вытекают следующие два наглядные необходимые и достаточные условия дифференцируемости заданной функции
Из геометрического смысла производной функции, определяемого равенством (11) и рис.5, вытекают следующие два наглядные необходимые и достаточные условия дифференцируемости заданной функции 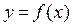 в заданной точке x:
в заданной точке x:
1) Существование касательной к графику функции в его точке с абсциссой x.
2) Не вертикальность этой касательной (ибо  не существует).
не существует).
Например, функция 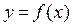 , график которой изображен на рис.7, не дифференцируема в точках x 1, x 2 и x 3.
, график которой изображен на рис.7, не дифференцируема в точках x 1, x 2 и x 3.
Действительно, точке x 1 соответствует на графике функции точка M 1 с вертикальной касательной. Точке x 2 (точке максимума функции) соответствует остроконечная вершина M 2, касательная в которой не существует. Точке x 3 соответствует точка M 3 – точка излома графика функции, в которой тоже касательная не существует.
Во всех же остальных точках M графика функции касательную к графику провести можно, и она не вертикальна. Значит, для всех остальных x, отличных от (x 1; x 2; x 3), существует производная функции. То есть во всех остальных точках x функция 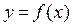 дифференцируема.
дифференцируема.
Непрерывность функций.
Определение. Функция у=f(x) называется непрерывной при значении х=х0 (или в точке х0), если она определена в некоторой окрестности точки х0 (очевидно, и в самой точке х0) и если  или, что то же самое,
или, что то же самое, 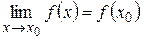 .
.
Геометрически непрерывность функции в данной точке означает, что разность ординат графика функции у=f(x) в точках 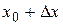 и х0 будет по абсолютной величине произвольно малой, если только
и х0 будет по абсолютной величине произвольно малой, если только 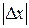 будет достаточно мало.
будет достаточно мало.
Для непрерывных функций справедливы следующие теоремы, регламентирующие операции с этими функциями:
Теорема 1: Если функции  и
и 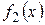 непрерывны в точке х0, то сумма
непрерывны в точке х0, то сумма 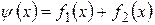 также есть непрерывная функция в точке х0.
также есть непрерывная функция в точке х0.
Теорема 2: Произведение двух непрерывных функций есть функция непрерывная.
Теорема 3: Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.
Теорема 4: Если 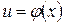 непрерывна при
непрерывна при  и f(u) непрерывна в точке
и f(u) непрерывна в точке 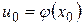 , то сложная функция
, то сложная функция 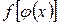 непрерывна в точке х0.
непрерывна в точке х0.
Еще три теоремы описывают свойства непрерывных функций:
Теорема 5: Если функция y=f(x) непрерывна на некотором отрезке 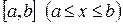 , то на отрезке
, то на отрезке 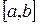 найдется по крайней мере одна точка
найдется по крайней мере одна точка  такая, что значение функции в этой точке будет удовлетворять соотношению
такая, что значение функции в этой точке будет удовлетворять соотношению , где х – любая другая точка отрезка, и найдется по крайней мере одна точка х2 такая, что значение функции в этой точке будет удовлетворять соотношению
, где х – любая другая точка отрезка, и найдется по крайней мере одна точка х2 такая, что значение функции в этой точке будет удовлетворять соотношению 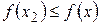 . Значение функции
. Значение функции  будем называть наибольшим значением функции y=f(x) на отрезке
будем называть наибольшим значением функции y=f(x) на отрезке 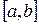 , значение функции
, значение функции 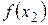 будем называть наименьшим значением функции на отрезке
будем называть наименьшим значением функции на отрезке 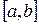 . (см. рис. 8)
. (см. рис. 8)

Рис. 8.
Теорема 6: Пусть функция 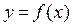 непрерывна на отрезке
непрерывна на отрезке 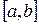 и на концах этого отрезка принимает значения разных знаков, тогда между точками а и b найдется по крайней мере одна точка х=с, в которой функция обращается в нуль:
и на концах этого отрезка принимает значения разных знаков, тогда между точками а и b найдется по крайней мере одна точка х=с, в которой функция обращается в нуль: 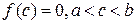 .
.
Геометрический смысл этой теоремы в том, что график непрерывной функции 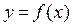 , соединяющий точки
, соединяющий точки 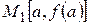 и
и 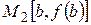 , где
, где  и
и 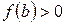 (или
(или 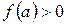 и
и 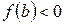 ) пересекает ось ох по крайней мере в одной точке.
) пересекает ось ох по крайней мере в одной точке.
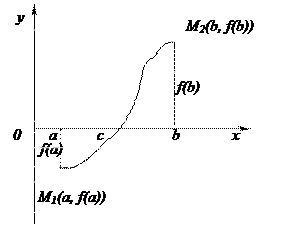
Рис.9.
Теорема 7: Пусть функция 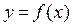 определена и непрерывна на отрезке
определена и непрерывна на отрезке 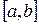 . Если на концах этого отрезка функция принимает неравные значения
. Если на концах этого отрезка функция принимает неравные значения  , то каково бы ни было число
, то каково бы ни было число 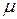 , заключенное между числами А и В, найдется такая точка х=с, заключенная между а и b, что
, заключенное между числами А и В, найдется такая точка х=с, заключенная между а и b, что 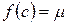 .
.
Геометрический смысл этой теоремы родственен теореме 6. В данном случае всякая прямая 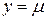 пересекает график функции
пересекает график функции 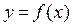 .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 3758; Нарушение авторских прав?; Мы поможем в написании вашей работы!