
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Затухающее колебание
|
|
|
|
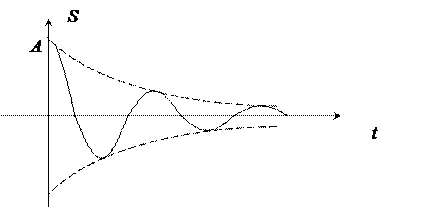 Простое гармоническое колебание не может продолжаться сколь угодно долго при постоянной амплитуде. В реальных условиях через некоторое время гармонические колебания прекращаются. Такие гармонические колебания в реальных системах называются затухающим колебаниями ( рис.2 ). К снижению амплитуды колебаний с последующим их прекращением приводит действие внешних сил, например, трения и вязкости. Эти силы уменьшают энергию колебаний. Они называются диссипативными силами, поскольку способствуют рассеиванию потенциальной и кинетической энергии макроскопических тел в энергию теплового движения атомов и молекул тела.
Простое гармоническое колебание не может продолжаться сколь угодно долго при постоянной амплитуде. В реальных условиях через некоторое время гармонические колебания прекращаются. Такие гармонические колебания в реальных системах называются затухающим колебаниями ( рис.2 ). К снижению амплитуды колебаний с последующим их прекращением приводит действие внешних сил, например, трения и вязкости. Эти силы уменьшают энергию колебаний. Они называются диссипативными силами, поскольку способствуют рассеиванию потенциальной и кинетической энергии макроскопических тел в энергию теплового движения атомов и молекул тела.
Рис.2
Величина диссипативных сил зависит от скорости тела. Если скорость  сравнительно мала, то диссипативная сила F прямо пропорциональна этой скорости
сравнительно мала, то диссипативная сила F прямо пропорциональна этой скорости 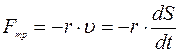 (6)
(6)
Здесь r - постоянный коэффициент, независимый от скорости или частоты колебаний. Знак минус указывает на то, что тормозящая сила направлена против вектора скорости движения.
Принимаясь во внимание действие диссипативных сил, дифференциальное уравнение гармонического затухающего колебания имеет вид: 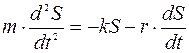 .
.
Перенеся все члены равенства в одну сторону, разделив каждый член на 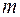 и заменяя
и заменяя  ,
,  , получим дифференциальное уравнение свободных гармонических затухающих колебаний
, получим дифференциальное уравнение свободных гармонических затухающих колебаний
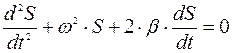 (7)
(7)
где 
 - коэффициент затухания, характеризующий затухание колебаний за единицу времени.
- коэффициент затухания, характеризующий затухание колебаний за единицу времени.
Решением уравнения является функция 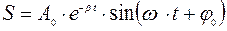 (8)
(8)
Уравнение (8) показывает, что амплитуда гармонического колебания уменьшается экспоненциально во времени. Частота затухающих колебаний определяется уравнением 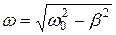 (9)
(9)
Если колебание не может происходить вследствие большого  , то система возвращается в свое положение равновесия по экспоненциальному пути без колебания.
, то система возвращается в свое положение равновесия по экспоненциальному пути без колебания.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 310; Нарушение авторских прав?; Мы поможем в написании вашей работы!