Задачи на плане и карте, решаемые по горизонталям

Надписи на горизонталях, указывающие их отметки, делаются таким образом, чтобы основания цифр были направлены в сторону понижения местности.

Хребет – вытянутая возвышенность, постепенно понижающаяся в одном направлении и имеющая два крупных ската (склона), пересечение которых образует ось хребта, называемую водораздельной линией.

Лощина – вытянутое углубление местности, постепенно понижающееся в одном направлении. Самая низкая линия лощины расположена вдоль ее, в пересечении двух скатов и образует водослив или тальвег.

Седловина – пониженная часть местности между двумя соседними возвышенностями. В горах седловины называют характерными точками рельефа, а водораздел и тальвег – характерными линиями рельефа.

1. Определение точек высот по горизонталям.

Если точка заданна на горизонтали, то ее отметка равна отметке горизонтали; если же точка находится между горизонталями, то высоту ее Н вычисляют по формуле:

Н = Н_о + h,

где Н_о – отметка ближайшей к точке горизонтали; h - превышение точки над этой горизонталей.

Считая, что высота между соседними горизонталями меняется пропорционально расстоянию между горизонталями (т.е. заложению), для вычисления h используется формула:

,

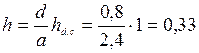
где а – заложение между горизонталями (2,4); d – расстояние от точки до ближайшей горизонтали (0,8); h _d.c – высота сечения рельефа (1).

Отсюда Н = 105,00 + 0,33 = 105,33.

2. Определение крутизны скатов. Масштаб заложений.

Мерой крутизны ската линии служит ее уклон i, который определяется тангенсом угла наклона ν.

Точка А и В находятся на горизонталях.

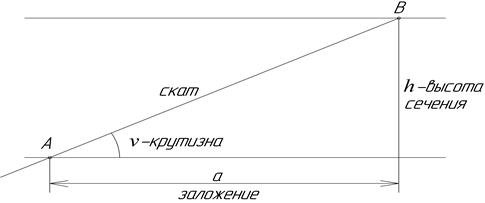
Из рисунка следует, что 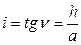, где h – высота сечения рельефа, м.; а – заложение, м (фактически горизонтальное проложение линии АВ.

Для быстрого определения уклона линии (в проценах – сотые доли, а в промилле – тысячные доли °/_°°) на практике обычно используются специальные номограммы, называемые графиком заложений, которые изображаются на крупномасштабных планах.

Для построения графика заложений перепишем формулу в таком виде:

а = h / i = h/tgn = h*ctgn.

Возьмем прямую линию АВ и отложим на ней произвольные (преимущественно равные) отрезки, подписывая их в порядке возрастания значений i, возможные на данном листе карты. Из точек делений восстановим перпендикуляры и отложим на них в масштабе карты величины заложений а, определенные по формуле. Концы этих перпендикуляров соединим плавной кривой.

Полученным графиком пользуемся следующим образом: раствором циркуля с карты берут заложение между двумя горизонталями по данному скату (горизонтальному проложению линии перпендикулярной к горизонталям), затем по графику находят такое место, где расстояние между кривой и прямой равно этому заложению и определяют соответствующий уклон. По этому графику можно решать и обратную задачу – определение величины заложения по заданному уклону.

На практике приходится также пользоваться углом наклона линии.

Угол наклона ν и заложение «а» определяют по формуле tg ν = h/a и

a = h · ctg ν.

Так как для каждого листа карты сечение рельефа h – величина заданная, то придавая ν последовательно различные значения, получим соответствующие значения для «а». Масштаб заложений для определения углов наклона строится также, как и для уклонов, только вместо i откладывают значение ν в градусах. Пользование графиком аналогичное.

Дата добавления: 2014-01-07