Введение векторных и скалярных потенциалов для мгновенных электромагнитных полей

Переменное электромагнитное поле в общем случае представляет собой более сложный объект, чем суперпозиция вихревого и потенциального полей, но оно может быть выражено через векторные и скалярные потенциалы.

Вернемся к УМ (3.1), но теперь предположим, что сторонние токи и заряды меняются во времени и связаны уравнением непрерывности (3.6).

Поскольку магнитных зарядов нет, мы, как и в стационарном случае, можем полагать, что векторное магнитное поле является вихревым и представлено как ротор некоторого вектора A ^e (см. определение (3.7)). Подставим соотношение (3.7) во второе УМ в (3.1). Это даст

,

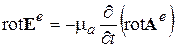или

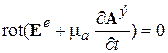(3.9)

Вектор, ротор которого равен нулю, может быть представлен градиентом некоторой потенциальной функции. В статике мы имели соотношение (3.3): Е = - grad φ. В электродинамике положим вектор, стоящий под знаком rot в (3.9), равным – grad j ^e:

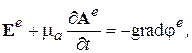
таким образом

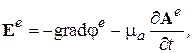(3.10)

Из (3.10) видно, что вектор Е не является чисто потенциальным, а содержит вихревую и потенциальную составляющие.

Исключим теперь Н ^e и Е ^e из 1-го УМ (3.1) с помощью (3.7) и (3.10). Получим

,

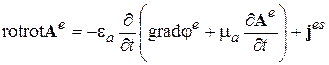Учитывая, что rotrot = - D + grad div, получим далее

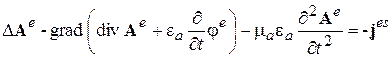(3.11)

Заметим теперь, что потенциалы А ^e и φ ^e уже не являются независимыми (это следует хотя бы из того факта, что сторонние токи и заряды связаны уравнением непрерывности). Это означает, что потенциал А ^e может содержать не только вихревую, но и «безвихревую» (потенциальную) составляющие. Поскольку условие (3.7) определяет только вихревую часть потенциала А ^e, прибавление к А ^e слагаемого вида grady не меняет Н ^e. Поэтому в (3.7) и (3.10) «безвихревая» часть потенциала А ^e не определена, а «потенциальная» часть вектора Е ^e слагается из двух величин – «безвихревой» части вектора А ^e и слагаемого gradj ^e.

Поскольку имеется свобода в выборе «безвихревой» части вектора А ^e, распорядимся ей следующим образом. Наложим на А ^e и gradj ^e такую связь, чтобы максимально упростить уравнение (3.11). Из (3.11) видно, что мы можем наложить условие

(3.12)

при этом уравнение (3.11) перейдет в волновое уравнение для векторного электрического потенциала (уравнение Даламбера)

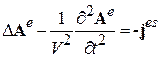. (3.13)

Здесь V= (ε _a μ _a)^-1/2 – скорость ЭМ волн в среде.

Дополнительная связь (3.12), наложенная на векторный потенциал А ^e и скалярный потенциал j ^e, называется условием калибровки Лоренца.

Обратим внимание на то, что в правой части уравнения (3.13) стоит только сторонний электрический ток, а производные тока отсутствуют. Это не только упрощает (по сравнению с аналогичными уравнениями для Е или Н) решение задач излучения антенн, но и облегчает физическую интерпретацию процессов излучения.

Предположим, что мы нашли решение векторного волнового уравнения (ВВУ) (3.13) для заданного распределения стороннего тока. Дальше надо найти поля Е и Н. Магнитное поле находится подстановкой вектора Н в (3.7). Чтобы найти электрическое поле, исключим скалярный потенциал φ ^e из (3.10), используя условие калибровки (3.12). Связь (3.12) можно рассматривать, как обыкновенное дифференциальное уравнение для потенциала φ ^e. Интегрируя его по времени, получим

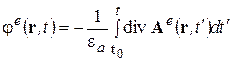(3.14)

Здесь для определенности принято, что сторонний ток включен в момент времени t ₀.

Подставив (3.14) в (3.10), получим, что электрическое поле может быть найдено с помощью соотношения

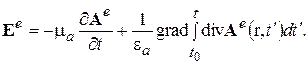(3.15)

Таким образом, для определения электрического и магнитного полей. создаваемых сторонним электрическим током, достаточно решить ВВУ (3.13) и далее найти поля Е и Н с помощью соотношений (3.7) и (3.15).

Аналогичные ВВУ и соотношения для электрического и магнитного полей, создаваемых сторонним магнитным током и определяемый через векторный магнитный потенциал, находятся с помощью принципа перестановочной инвариантности (см. [1], стр. 36-37). Соответствующие соотношения предлагается получить самостоятельно.

Дата добавления: 2014-01-07