Лекция 6. Тема: “ Анализ модели на устойчивость”

Тема: “ Анализ модели на устойчивость”

1. Анализ модели на устойчивость по отношению к изменениям запасов продукции. Двойственные оценки тесным образом связаны с оптимальным планом прямой задачи. Всякое изменение исходных данных прямой задачи может оказать влияние как на её оптимальный план, так и на систему двойственных оценок. Поэтому, чтобы проводить экономический анализ с использованием двойственных оценок, нужно знать их интервал устойчивости.

Свойство устойчивости в общем случае – это сохранение оптимальности решения при небольших изменениях параметров. Устойчивость модели играет важную роль на практике. Если значение оптимального решения резко изменяется при небольших отклонениях параметров, то такой моделью сложно пользоваться на практике, где изменения цен и запасов – явление обыденное.

При анализе устойчивости необходимо дать ответы на следующие вопросы.

1. На сколько могут быть увеличены запасы дефицитных ресурсов для улучшения оптимального плана при сохранении общей структуры решения?

2. На сколько могут быть снижены запасы дефицитных ресурсов при сохранении общей структуры оптимального решения?

3. Какие дефицитные ресурсы следует увеличивать в первую очередь?

4. На сколько могут быть снижены запасы недефицитных ресурсов при сохранении оптимальности полученного решения?

5. Каковы пределы изменения коэффициентов целевой функции, при которых не происходит изменения оптимального плана?

6. На сколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать дефицитный ресурс недефицитным и наоборот?

Предположим, что прямая задача имеет невырожденные опорные планы и хотя бы один из них является оптимальным.

Максимальное значение целевой функции прямой задачи будем рассматривать как функцию свободных членов системы линейных уравнений: .

Теорема. В оптимальном плане двойственной задачи значение переменной численно равно частной производной функции по данному аргументу, т.е.

Последнее равенство означает, что изменение значений величин 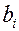приводит к увеличению или уменьшению . Это изменение определяется величиной и может быть охарактеризовано лишь тогда, когда при изменении величин 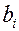значения переменных в оптимальном плане соответствующей двойственной задачи остаются неизменными. Поэтому представляет интерес определить такие интервалы изменения каждого из свободных членов системы линейных уравнений прямой задачи, в которых оптимальный план двойственной задачи не меняется. Это имеет место для всех тех значений , при которых столбец свободных членов последней симплекс-таблицы решения задачи не содержит отрицательных чисел, т.е. тогда, когда среди компонент вектора

нет отрицательных. Здесь В^-1 - матрица, обратная матрице В, составленной из компонент векторов базиса, который определяет оптимальный план задачи.

Пример 1. Для изготовления четырёх видов продукции предприятие использует три типа ресурсов. Нормы расхода ресурсов каждого типа на единицу продукции, их наличие и цена единицы продукции каждого вида приведены в таблице.

Тип ресурса	Нормы затрат сырья (кг) на единицу продукции	Наличие ресурса
А	В	С	D
I II III
Цена единицы продукции(ден.ед.)

Требуется:

а) сформулировать двойственную задачу и найти оптимальные планы прямой и двойственной задач;

б) найти интервалы устойчивости двойственных оценок по отношению к изменениям ресурсов каждого типа;

в) выявить изменение общей стоимости изготовляемой продукции, определяемой оптимальным планом её производства при уменьшении количества ресурса I типа на 60 ед. и увеличении количества ресурсов II и III типов соответственно на 120 и 160 ед.

Решение:

а) Предположим, что изделия видов А, В, С и D будут производиться соответственно в количествах ,,,.

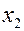Для определения оптимального плана производства продукции следует найти решение задачи, состоящей в определении максимального значения функции

при ограничениях

(1)

Припишем единице каждого из используемых ресурсов двойственную оценку, соответственно равную 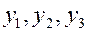. Тогда общая оценка сырья, используемого на производство продукции, составит

при условиях

(2)

Задачи (1) и (2) образуют пару двойственных задач. Решение прямой задачи даёт оптимальный план производства изделий А, В, С и D, а решение двойственной – оптимальную систему оценок сырья, используемого для производства этих изделий.

Чтобы найти решение этих задач, следует сначала отыскать решение какой-либо одной из них. Так как система ограничений задачи (1) содержит лишь неравенства вида «», то лучше сначала найти решение этой задачи. Её решение приведено в таблице.

Базис
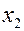
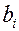
f	-9	-6	-4	-7
Базис
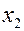
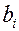
			-8		-4
f		-6
Базис
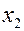
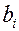
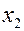
			-4		-2		-1/2 1/2
f			-10		-3
Базис
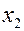
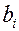
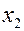
			-3/2 7/2			-1/2 1/2	1/4 -1/4
f			1/2			3/2	9/4

Из последней симплекс-таблицы видно, что оптимальным планом производства изделий является такой, при котором изготавливается 95 изделий А и 210 изделий В. При данном плане производства остаётся неиспользованным 85 ед. ресурса II типа, а общая стоимость изделий равна 2115 руб. Из таблицы также видно, что оптимальным решением двойственной задачи является

б) Определим интервалы устойчивости двойственных оценок по отношению к изменениям ресурсов каждого типа. Для этого найдём компоненты вектора

и определим, при каких значениях они не отрицательны. Прежде чем это сделать, отметим, что матрица В^-1, обратная матрице В, составленной из вектор-столбцов, соответствующих базисным переменным , , 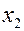в оптимальном плане задачи (1), записана непосредственно на основании данных таблицы, а именно: элементы матрицы В^-1 взяты из вектор-столбцов, соответствующих переменным ,,, образующим первоначальный базис.

Условие неотрицательности компонент указанного выше вектора приводит к следующей системе неравенств:

(3)

1. Это означает, что если количество ресурсов I типа будет уменьшено в пределах 85 ед., то оптимальный план двойственной задачи не изменится.

2. Таким образом, если количество ресурсов II типа принадлежит промежутку , а количество остальных ресурсов остаётся первоначальным, то оптимальный план двойственной задачи не изменяется.

3. Таким образом, если количество ресурсов III типа принадлежит промежутку , а количество остальных ресурсов остаётся первоначальным, то оптимальный план двойственной задачи не изменяется.

Замечание 1. Если изменяются одновременно, то исследование несколько усложняется, поскольку в данном случае нужно найти многогранник решений системы линейных неравенств.

в) В данной задаче одновременно изменяется количество ресурсов всех трёх типов. Количество ресурса I типа уменьшается на 60 ед. (), а количество ресурсов II и III типов соответственно увеличиваются на 120 и 160 ед. (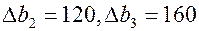). Следовательно, надо выяснить, остаётся ли оптимальным планом двойственной задачи (2) при указанном изменении количества ресурсов или нет. Для этого нужно проверить, удовлетворяют ли данные системе неравенств (3). Подставим в неравенства (3) вместо их значения –60, 120, 160:

Следовательно, несмотря на изменение объёмов ресурсов в указанных размерах, оптимальным планом двойственной задачи остаётся .

Данное заключение позволяет воспользоваться теоремой для определения приращения максимального значения функции 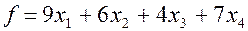при указанных изменениях количества ресурсов. В этом случае

Это означает, что уменьшение количества ресурса I типа на 60 ед. и увеличение количества ресурсов II и III типов соответственно на 120 и 160 ед. приведёт к возможности построения такого плана производства продукции, реализация которого обеспечит выпуск изделий на 540 руб. больше, чем при плане производства продукции, обусловленном первоначальным количеством ресурсов.

Дата добавления: 2014-01-07