Займёмся выводом, пока формальным, энергетических соотношений, а потом укажем, в чём именно заключается постулат, относящийся к этим соотношениям

Энергетические соотношения в электродинамике.

ЛЕКЦИЯ 4.

Исправление: в последнем интеграле (4.17) в подинтегральном выражении знак минус

Ранее мы упоминали, что к постулатам, представляющим собой формулировку УМ, необходимо добавить постулат об энергии э/м поля.

Уравнения баланса энергии для нестационарных полей.

Запишем нестационарные УМ:

* E

(4.1)

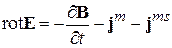* H

Преобразуем систему (4.1) следующим образом: умножим скалярно 1-е УМ на вектор Е, 2-е - на вектор Н и вычтем из 2-го уравнения 1-е.

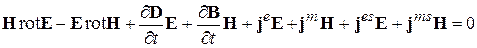(4.2)

Воспользуемся формулой векторного анализа

и перепишем соотношение (4.2) в виде:

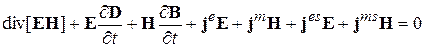(4.3)

Воспользуемся материальными уравнениями D= ε_а E, B= μ _а H, j ^e = σ_e E, j ^m =σ _m H, где - константы, и подставим МУ в (4.3). В результате получим:

(4.4)

Введём обозначение . Этот вектор называется вектором Пойнтинга. Если Е и Н ортогональны, П образует с Е и Н тройку ортогональных векторов. В общем случае П ортогонален плоскости, в которой лежат векторы Е и Н.

Окончательно соотношение (4.4) примет вид:

(4.5)

Это соотношение называют теоремой Пойнтинга в дифференциальной форме для мгновенных значений векторов поля.

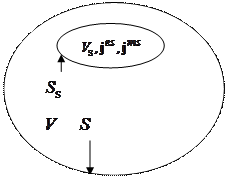
Предположим, что источники поля j ^{’ es}, j ^{’ ms}

заключены в объёме V _s, ограниченном

поверхностью S_s. Окружим объём

источников поверхностью S,

Объём внутри S обозначим V: .

Далее проинтегрируем соотношение (4.5)

по объёму V и применим теорему Гаусса:

рис.4.1

В результате получим

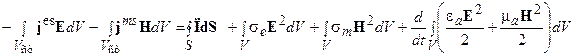
(4.6)

Выражение (4.6) представляет собой закон сохранения энергии электромагнитного поля. Его называют теоремой Пойнтинга в интегральной форме для мгновенных значений векторов электромагнитного поля.

Рассмотрим отдельные слагаемые (4.6), прежде всего:

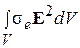и .

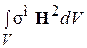Величины σ _e Е² и 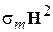имеют размерность Вт / м³

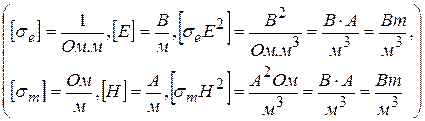
т.е. представляют собой объёмные плотности мощности. Величина σ _e Е ² определяется электрическими потерями и представляет собой объёмную плотность мощности электрических потерь, аналогично σ _m Н ² представляет собой объёмную плотность мощности магнитных потерь в среде. Интегралы и соответственно, представляют собой мгновенные мощности электрических и магнитных потерь в объёме V и имеют размерность Вт. Поэтому и все остальные интегралы в (4.6) имеют размерность Вт.

Постулируем теперь, что величина w = w^e + w ^m является объёмной плотностью энергии электромагнитного поля и слагается из объёмной плотности энергии электрического поля и объёмной плотности энергии магнитного поля 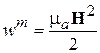[1]. Этот постулат вводится по аналогии с определением энергий электрического поля в электростатике и магнитного поля в магнитостатике. Соответственно величина есть энергия электромагнитного поля в объёме V, тогда имеет размерность мощности. Величина также имеет размерность мощности. Вектор имеет размерность Вт/м²и определяет мгновенное значение вектора плотности потока мощности. Величина 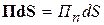, где 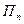- нормальная к площадке 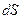компонента П, определяет поток мощности через площадку 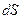на поверхности S. Интеграл 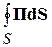определяет полный поток мощности через поверхность S. Наконец, величина, стоящая в левой части равенства (4.6), представляет собой мгновенную мощность сторонних токов. Таким образом, (4.6) представляет собой уравнение баланса энергии электромагнитного поля, имеющее следующий смысл: мгновенная мощность сторонних токов равна сумме мгновенной мощности электромагнитного поля, накапливаемой в объёме V, мгновенных мощностей потерь в объёме V и мощности, уходящей через поверхность S из объёма V. Обратим внимание на то, что интегралы в левой части берутся только по объёму сторонних токов.

Перепишем уравнение (4.6) в виде:

(4.7)

Здесь - работа сторонних токов, 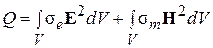- тепловые потери энергии электрического и магнитного полей, 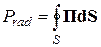- потери на излучение. Слева в (4.7) стоит приращение энергии э/м поля . Соотношение (4.7) можно трактовать следующим образом: приращение энергии э/м поля W в объёме V равно избытку работы сторонних токов j ^es, j ^ms над тепловыми потерями и потерями на излучение.

Величина Q определяет тепло, выделяющееся в объёме V. Эта величина доступна непосредственному измерению, что даёт возможность проверять правельность теории.

Замечание. В приведённой формулировке уравнение баланса энергии не учитывает возможность потерь энергии при диэлектрической поляризации и намагничивании среды (для их учёта нужны более сложные МУ).

Случай монохроматических полей.

В этом случае можно вывести теорему Пойнтинга для монохроматических полей.

Но прежде чем дать её вывод, рассмотрим простую электрическую цепь, на которой можно понять, как формулировать энергетические соотношения, используя комплексные амплитуды

Рассмотрим вспомогательную задачу, поясняющую, как определить энергетические соотношения по комплексным амплитудам. (Если этот материал знаком по курсу «Основы теории цепей», можете пропустить этот материал). см. рис. 4.2.

R

Источник e_ст C

ЭДС

L

Рис. 4.2.

Пусть ЭДС меняется по гармоническому закону:

(4.8)

Уравнение для тока в цепи рис.(4.2) имеет вид

Дифференцируя по t, получим

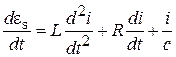(4.9)

Выражение для тока найдём, положив

(4.10)

Здесь 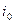и неизвестны. Подставим (4.10) в (4.9). Так как

, ,

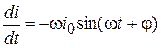то (4.9) переходит в

Разложим тригонометрические функции и по формулам синуса и косинуса суммы двух углов. После упрощения получим,

где

,

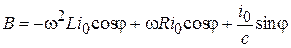
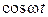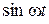
Приравняв множители при и к нулю: 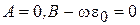, получим выражения для амплитуды и фазы тока

, .

Количественные значения 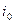и нам сейчас не важны, важно, что подстановкой (4.10) в уравнение (4.9) они находятся.

Найдём теперь мгновенную мощность, отдаваемую источником ЭДС

Практически чаще всего интересуются не мгновенной мощностью, а средней за период ВЧ колебания . Именно эта величина измеряется с помощью приборов.

Средняя за период мощность равна:

(4.11)

Получим то же выражение с помощью метода комплексных амплитуд.

Соотношения между мгновенными значениями и комплексными амплитудами:

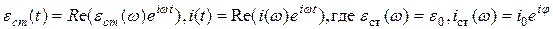
Рассмотрим величину и найдём величину :

Это выражение совпадает с (4.11). Таким образом средняя за период мощность потерь (или активная мощность) равна:

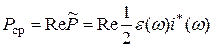(4.12)

Аналогично можно показать, что величина определяет реактивную мощность в цепи. Она равна

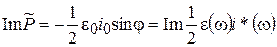(4.13)

Таким образом, методом комплексных амплитуд можно вычислить мощность потерь и реактивную мощность в цепи.

Будем использовать аналогичные (4.12) и (4.13) выражения для определения энергетических характеристик монохроматических полей.

Возьмём УМ для комплексных амплитуд полей в виде:

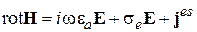(4.14а)

(4.14б)

Возьмём комплексно сопряжённое уравнение (4.14а) и умножим скалярно на Е:

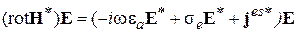
Далее возьмём уравнение (4.14б), умножим его скалярно на Н *

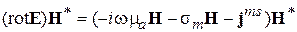
и вычтем из 2-го соотношения 1-е. В результате получим:

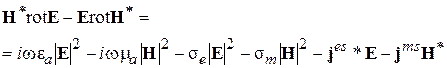
Здесь учтено, что .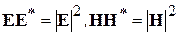

Кроме того, используем известное векторное тождество

.

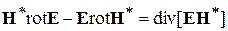После этого получим:

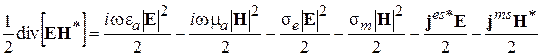(4.15)

Это теорема Пойнтинга (закон сохранения энергии) для комплексных амплитуд полей в дифференциальной форме. Здесь левая и правая части равенства были умножены на ½, чтобы в итоге получить среднюю за период мощность.

Перейдём, как и в случае мгновенных значений поля, к интегральной форме теоремы Пойнтинга для комплексных амплитуд полей. Проинтегрируем равенство (4.15) по объёму V и воспользуемся теоремой Гаусса. Тогда левая часть соотношения (4.15) преобразуется к виду:

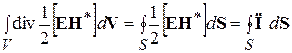
Здесь мы ввели вектор Пойнтинга в комплексной форме:

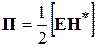(4.16)

В результате получим:

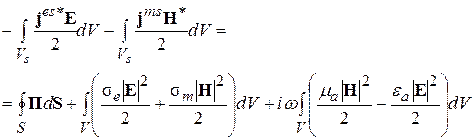(4.17)

Это теорема Пойнтинга в интегральной форме или уравнение баланса энергии для комплексных амплитуд полей.

Выделим в этом соотношении действительную часть:

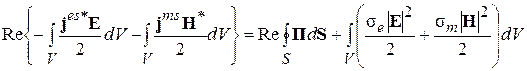(4.18)

Левая часть равенства (4.18) определяет активную (среднюю за период) мощность, отдаваемую сторонними источниками в объём V. Слагаемые правой части показывают, на что тратится эта мощность. Первое слагаемое в правой части (4.18) определяет среднюю мощность э/м поля, излучаемую из объема V через поверхность S. Два вторых слагаемых определяют среднюю мощность потерь на нагрев среды в объёме V. Таким образом, можно записать соотношение (4.18) в обобщённой форме

Р _{ср стор} = Р _{ср излучения} + Р _{ср тепловых потерь} (4.18а)

Выделим в соотношении (4.17) мнимую часть

(4.19)

Левая часть соотношения (4.19) определяет реактивную мощность, отдаваемую сторонними источниками в объём V. Первое слагаемое в правой части определяет реактивную мощность, которая проходит через поверхность S и устанавливается вне объема V. Второе слагаемое в правой части определяет реактивную мощность, которая устанавливается внутри объёма V.

Предположим, что объём V экранирован поверхностью S так, что

. Это может быть в двух случаях: а) если существует физический экран (металл), либо б) если поверхность S достаточно удалена от объёма сторонних источников V_{c т.} Во втором случае (излучение есть), но , когда радиус поверхности S растёт. В этом случае реактивная мощность сторонних источников тратится только на создание реактивной мощности внутри объёма V.

Можно показать также, что средние за период плотности энергии электрического и магнитного полей равны

,

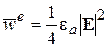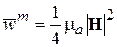
Поэтому

, (4.20)

где

, .

Таким образом, реактивная мощность в объёме V равна умноженной на 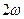разности между средними значениями энергий магнитного и электрического полей в объёме V. С учётом этого из (4.19) следует вывод, что при и 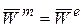в установившемся режиме реактивная мощность в объём V от сторонних источников не поступает.

Замечание ([2], § 92). Как показывает анализ физических экспериментов, непосредственная проверка на опыте возможна лишь по отношению к теореме Пойнтинга в интегральной форме, применённой к замкнутым поверхностям. Тем не менее вектор Пойнтинга отождествляют с плотностью потока энергии в данной точке пространства. Эта интерпретация вектора Пойнтинга позволяет наглядно проследить движение энергии электромагнитного поля.

Литература к лекции 4

1. Марков Г.Т., Петров Б.М., Грудинская Г.П. Электродинамика и распространение радиоволн. М. 1979. См. гл. 1, §§ 1.5, 1.7.

2. Тамм И.Е. Основы теории электричества. М.: Наука. 1966. 624 с.

См. гл. 7, §§ 91-93.

Дата добавления: 2014-01-07