ЛЕКЦИЯ №1 часть 2

Определение перемещений в балках при изгибе

Балки должны удовлетворять не только условиям прочности, но и условиям жесткости. Небольшие прогибы балок не должны превышать допускаемой величины. (Это вторая задача сопромата – расчет на жесткость).

Фактический прогиб

ƒmax.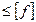

- допускаемый прогиб, устанавливается техническим условием или нормалями в отрасли.

Для мостовых и подкрановых балок:

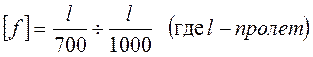
Для балок перекрытий .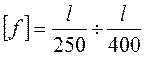

Также определение перемещений в балках необходимо для расчета статически неопределенных систем.

Введем ряд понятий и обозначений. Рассмотрим балку под действием силы Р.

Первоначальная прямолинейная ось балки – недеформированная ось.

При деформации ось балки изгибается (изогнутая ось называется упругой линией балки).

Балка изгибается при плоском поперечном изгибе в силовой плоскости.

Покажем утрированное изображение балки, т.к. для жестких балок не вооруженным глазом перемещение не обнаружить.

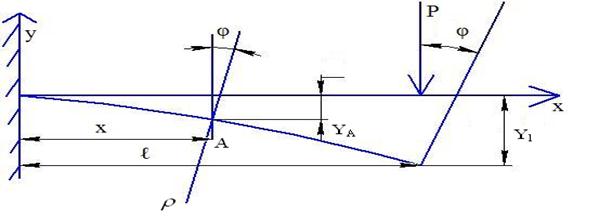
Возьмем точку А на оси балки на расстоянии Х от заделки.

Перемещения точек вдоль оси балки представляют собой малые высоких порядков, по сравнению с вертикальными перемещениями точек. Поэтому осевыми перемещениями этих точек пренебрегаем. Введем оси Х и Y, следовательно перемещение точки А =

Перемещения центра тяжести сечения по перпендикуляру к недеформированной оси балки называется прогибом и обозначается буквой y.

Проведем касательную и нормаль к деформированной оси. Угол, на который поворачивается сечение по отношению к первоначальному положению, называется углом поворота сечения.

Точка О – центр кривизны, ρ – радиус кривизны в данной точке.

На конце балки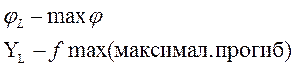

Имеем связь 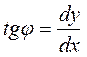, но угол φ<1º (для реальных балок), поэтому ;

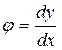
Раньше при определении изгиба получали формулу для кривизны

(*)

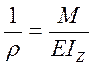Из геометрии кривизна кривой определяется как

(**)

При малых перемещениях второй член в знаменателе мал и им можно пренебречь. Приравнивая правые части выраженной (*) и (**) и принимая во внимание принятое допущение получим

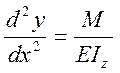(1) Приближенное дифференциальное уравнение изогнутой оси балки.

Знак ± в формуле опущен. Такая запись возможна только в том случае, если ось у всегда направлена вверх.

Покажем

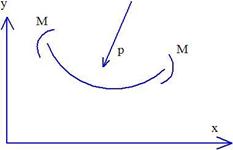М>0 >0

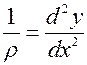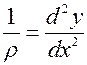М<0 <0

Проинтегрируем уравнение (1)

(2)

Это уравнение углов поворота сечений балки.

Еще раз проинтегрируем

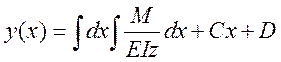(3)

Уравнения прогибов балки.

C и D постоянные интегрирования.

Они определяются из условий крепления балки на границах участков.

Пример использования этих уравнений

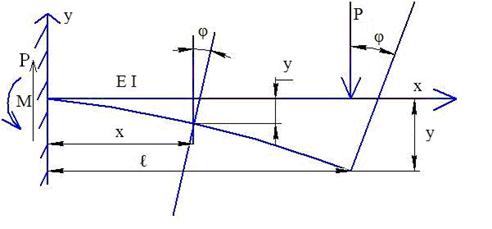
В заделке M=Pl

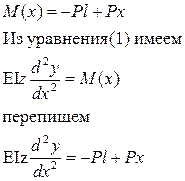
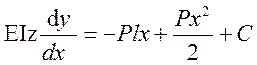
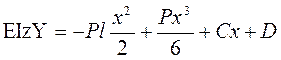
Найдем C и D из условия крепления балки при х=0 у=0,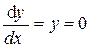

Если 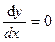, С =0

Если у=0, D =0

Следовательно:

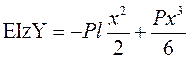
При x=ℓ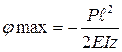

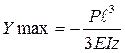
Способ носит название – метод непосредственного интегрирования дифференциального уравнения изогнутой оси балки.

Метод непосредственного интегрирования дифференциального уравнения балки имеет недостатки:

1. Требуется определять постоянные интегрирования.

2.Число постоянных интегрирования равно удвоенному числу участков.

На практике определение перемещений в балках производится методом начальных параметров. В этом методе требуется определить две постоянные интегрирования независимо от числа участков.

Дата добавления: 2014-01-07