Минимизировать суммарные затраты

Удовлетворить весь спрос потребителей

Вывести весь груз поставщиков (запасы)

Построение математической модели:

Пусть х_{ij –} количество груза, перевозимого от i-го исх. пункта к j-му пункту потребления.

х₁₁ + х₁₂+ ….+х_1n= а₁

х₂₁ + х₂₂+ ….+х_2n= а₂ →все грузы должны быть вывезены

……………………..

х_m1 + х_m2+ ….+х_mn= а_m

х₁₁ + х₂₁+ ….+х_m1= b₁

х₁₂ + х₂₂+ ….+х_m2= b_{2 →} весь спрос удовлетворен

…………………….

х_1n + х_2n+ ….+х_mn= b_n

F =

Замечание:

Если 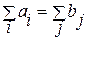, то задача называется закрытой, в противном случае - открытой. Доказано, что закрытая транспортная задача всегда имеет оптимальное решение.

§ 8 Метод потенциалов решениятранспортной задачи.

Метод потенциалов предполагает, исходя из начального опорного плана, построение конечной последовательности опорных планов, сходящихсяк оптимальному плану.

Разберем этот метод на конкретном примере:

На трех железнодорожных станциях Череповца сосредоточено топливо для пяти цехов завода Северсталь. Необходимо составить оптимальный план перевозок топлива. Исходные данные заданы в транспортной таблице стандартного вида:

Поставщ.						ЗАПАСЫ
Потребит.
СПРОС

Тр. задача закрытая (почему?).

1. Нахождение начального опорного плана (угловой точки).

Используется метод минимальной стоимости. Его суть:

а) находим клетку с минимальной стоимостью и в максимально возможной степени удовлетворяем спрос соответствующего потребителя. Результат записываем в левый нижний угол клетки.

Пост.						ЗАПАСЫ
Потр.
СПРОС

нижняя 4

б) правило: “там где 0 вычеркиваем”

в) среди всех невычеркнутых клеток вновь находим клетку с минимальной стоимостью и вновь повторяем алгоритм.

в) контроль: общее число занятых клеток равно

m + n – 1.

г) F = 20*7 + 80*2+ 100*4 + 30*6 + 70*4 + 150*2 + 50*5= 1710

Начальный опорный план- в левом нижнем углу клеток.

2. Проверка опорного плана на оптимальность.

Проверка на оптимальность осуществляется с помощью потенциалов во вновь составленной таблице.

Пост.						U
Потр.
	7 -	4 +
	+ 6	-				-1
						-2
V

ПРАВИЛО 1: для всех занятых клеток должно быть:

u _i + v _j = c _{i j} (1)

(сумма потенциалов равна стоимости)

ПРАВИЛО 2: для всех свободных клеток должно быть:

u _i + v _j ≤ c _{i j} (2)

Условие оптимальности нарушено в клетке (1, 2)!

Итак, полученный опорный план не оптимален!

Экономический смысл потенциалов:

Потенциалы u и v можно рассматривать как платежи

поставщиков и потребителей некоторому третьему лицу- назовем его “ перевозчиком”.

Формула (2) означает, что при оптимальном плане перевозок стороны не хотят переплачивать сверх установленного тарифа.

С другой стороны, перевозчик, установив оптимальный план, хочет получить максимум, т.е. весь тариф полностью (формула (1)).

3. Переход к новому опорному плану, лучшему, чем предыдущему.

Находим клетку, в которой условие оптимальности нарушено в наибольшей степени. В нашем случае это клетка (1,2). Далее

а) помечаем эту клетку знаком + и строим цикл, начинающийся и заканчивающийся в этой же клетке.

Цикл- это замкнутая ломаная линия, состоящая из горизонтальных и вертикальных отрезков, соединяющих некоторые занятые клетки.

Такой цикл всегда существует и только один!

б) размечаем вершины цикла знаками - + - … считая от исходной клетки.

в) находим, по всем клеткам помеченым знаком - наименьшую перевозку. Обозначим ее α. У нас α = 20.

г) двигаясь по циклу, прибавляем α к клеткам со знаком + и вычитаем ее из клеток со знаком -.

Получающиййся “лишний нуль” стираем.

Результаты записываем в новую таблицу.

Пост.						U
Потр.
						-1
V

Не забываем проверять условие: число занятых клеток = m+n -1.

4. Проверка опорного плана на оптимальность.

Вновь находим потенциалы и проверяем условие (2).

Условие оптимальности выполнено.

Получен оптимальный план перевозок!

F_min = 20*4 + 80*2 + 100*4 + 50*6 + 50*4 + 150*2 + 50*5 = 1690

х₁₂ = 20

х₁₃ = 80

х₁₅ = 100

х₂₁ = 50

х₂₂ = 50

х₂₄ = 150

х₃₁= 50

Графическая иллюстрация.

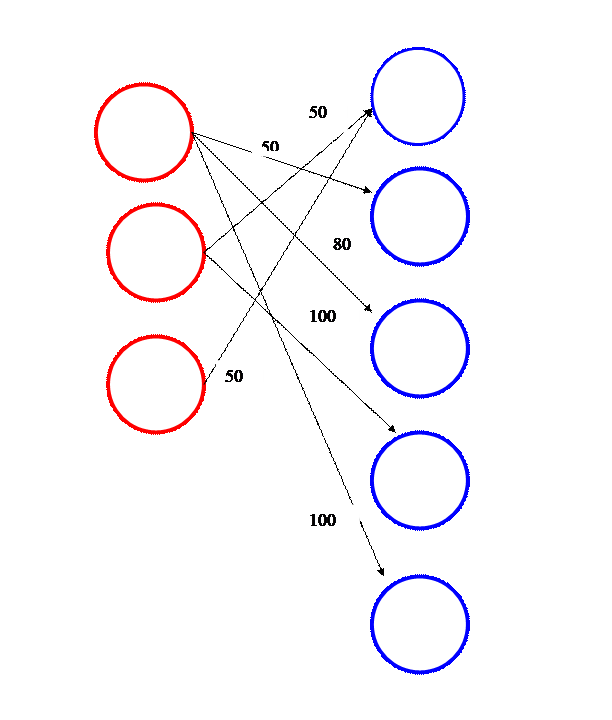
§ 9 Особенности решения открытой транспортной задачи:

Напомним, что в открытой транспортной задаче сумма запасов не равна сумме спроса:

1) пусть 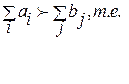сумма запасов превышает суммарный спрос.

Вводим фиктивного потребителя- в таблице это означает добавление в таблицу столбца. Приписываем этому потребителю спрос 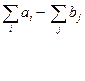. В соответствующих клетках тарифы равны нулю. Задача становится закрытой.

2) пусть 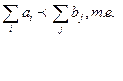сумма запасов меньше суммарного спроса.

Вводим фиктивного поставщика - в таблице это означает добавление в таблицу строки. Приписываем этому поставщику запасы 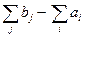. В соответствующих клетках тарифы равны нулю. Задача становится закрытой.

Пример:

Решить транспортную задачу:

Пост.					ЗАПАСЫ
Потр.
СПРОС

Задача открытая, т.к. суммарные запасы меньше суммарного спроса.

Следуя рекомендации введем фиктивного поставщика.

Пост.					ЗАПАСЫ
Потр.
4^*
СПРОС

1. Нахождение начального опорного плана (угловой точки).

Отметим, что фиктивные клетки следует рассматривать в последнюю очередь.

Пост.					ЗАПАСЫ
Потр.
4^*
СПРОС

Проверяем условие m+ n- 1.

2. Проверка опорного плана на оптимальность.

Проверка на оптимальность осуществляется с помощью потенциалов во вновь составленной таблице.

Пост.					U
Потр.
4^*					-2
V

Условие оптимальности выполнено!

Получен оптимальный план перевозок!

F_max = 35*1 + 5*2 + 20*3 + 40*3 + 25*4 + 65*2 + 0 =455

х₁₂ = 35

х₂₁ = 20

х₂₃ = 40

х₃₁ = 25

х₃₄ = 65

х₄₃ = 10

Заметим, что третий потребитель ничего не получит!

Выполним вычисления в EXCEL.

Дата добавления: 2014-01-07