Сочетания

Пример 5.6. Из отделения в 5 курсантов необходимо назначить двоих для патрулирования территории института. Сколькими различными способами можно сделать такой выбор?

Решение. В задаче мы не можем применить правило произведения, найдя сначала число способов выбора 1-го курсанта – 5, а потом – второго – 4 и перемножив их, получив 20 различных нарядов. Причиной этого является то, что порядок выбора курсантов в наряд не имеет значения. Важен лишь состав наряда. Поэтому будем решать задачу следующим образом.

Обозначим курсантов следующим образом: a, b, c, d, e. Из пяти курсантов составим всевозможные пары для несения службы в патруле:

ab, ac, ad, ae,

bc, bd, be,

cd, ce,

de.

Т.к., к примеру, пара ab и bа идентичны, то всего получается 10 различных вариантов наряда.

Такой способ решения является весьма нерациональным. Ведь если было бы необходимо выбрать наряд в 7 курсантов из 20, то (как это будет показано ниже) количество различных вариантов наряда составило бы более 77 тысяч. А попытка получить решение подобным образом окончилась бы полным провалом.

Для вывода общих формул комбинаторики рассмотрим вопрос: что общего и в чем заключаются отличия в примерах 5.4 и 5.6. Итак, в этих примерах идет речь о некотором конечном множестве элементов и о количестве его подмножеств, удовлетворяющих заданным требованиям. Так, в примере 5.4 рассматривалось множество курсантов учебной группы, состоявшее из 25 элементов (курсантов), и требовалось найти количество подмножеств, состоящих из 2 элементов (командир взвода и его заместитель). В примере 5.6 из пятиэлементного множества выделялись двухэлементные подмножества (наряды) и подсчитывалось их число.

Различие примеров заключалось в том, что в примере 5.6 подмножества различались лишь составом курсантов, а порядок элементов не имел значения. Действительно, наряд, состоящий из курсантов Иванова и Петрова, ни чем не отличался от наряда, состоящего из курсантов Петрова и Иванова. В примере 5.4, напротив, подмножества отличались не только своим составом, но и порядком расположения элементов. Назначение Иванова – командиром взвода, а Петрова – заместителем командира взвода отличается от комбинации выбора: Петров – командир взвода, Иванов – его заместитель.

Если подмножества различаются не только составом элементов, но и порядком следования элементов, то они называются упорядоченными. Неупорядоченные подмножества различаются только составом входящих в них элементов. Так, у множества, состоящего из 5 элементов, имеется 10 неупорядоченных подмножеств, состоящих из 2 элементов (см. пример 5.6), и 20 упорядоченных.

Пусть имеется множество, состоящее из n элементов. Каждое его неупорядоченное подмножество, содержащее k элементов, называется сочетанием из n элементов по k элементов. Из определения вытекает, что .

Сочетания из n элементов по k элементов – все k - элементные подмножества n – элементного множества, различающиеся только составом элементов. Подмножества, отличающиеся друг от друга порядком следования элементов, не считаются различными. Например, для четырехэлементного множество a, b, c, d сочетаниями из 4 элементов по 3 элемента являются подмножества: abc, abd, acd, bcd.

Число всех сочетаний из n по k элементов обозначается специальным символом . (Читается: «число сочетаний из n по k» или «С из n по k»). C – первая буква французского слова «combinasion» - «сочетание».

Число сочетаний из n по k элементов определяется следующей формулой:

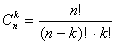. (5.2)

Здесь мы использовали функцию факториала:

(n  N), 0!=1.

Запись читается: «n факториал».

1!=1, 2!=1 2, 3!=1 2 3=6, 4!=1 2 3 4=24, 5!=1 2 3 4 5=120, 6!=1 2 3 4 5 6=720 и т.д.

Из приведенных выше вычислений факториала ряда чисел очевидно следующее равенство:

n!=(n -1)! n для n >0.

Представив n! в виде n!=(n-k)!(n-k +1)(n-k +2)…(n-1) n и сократив числитель и знаменатель формулы (5.2) на (n-k)!, получим следующую формулу для числа сочетаний из n по k элементов:

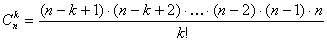(для k >0) (5.3)

Если k =0, то . Действительно, существует только одно пустое (не содержащее элементов) подмножество множества из n элементов.

Пример 5.7. Сколько различных нарядов, состоящих из 7 курсантов, можно составить из взвода численностью 20 курсантов?

Решение. Количество различных нарядов равно числу сочетаний из 20 по 7 - 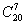. По формуле (5.3) получим

.

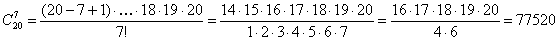Итак, количество различных нарядов равно 77520.

Пример 5.8. Сколько поединков по борьбе должны быть проведены между 15 спортсменами, если каждый из них должен встретиться с каждым.

Решение. Должно состояться столько поединков, сколько существует двухэлементных подмножеств у множества, состоящего из 15 элементов, т.е. их число равно 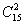. По формуле (5.3) получаем .

Итак, при встрече каждого из 15 спортсменов с каждым должно состояться 105 поединков.

Дата добавления: 2014-01-07