Геометрическое и статистическое определения вероятности

Вычисление вероятности с помощью классического определения

Решение задач с помощью классического определения можно представить в виде следующей схемы.

1. Во-первых, необходимо четко представить, в чем состоит испытание (эксперимент, опыт), в результате реализации которого происходит или не происходит интересующее нас случайное событие А.

2. Во-вторых, мы должны определить, сводится ли это испытание к схеме случаев. Для этого:

а) нужно сформулировать, что можно рассматривать в качестве элементарных исходов испытания (обычно при решении задач в качестве элементарных исходов берут самые простые исходы, которые уже нельзя «расщепить», хотя это вовсе и не обязательно);

б) элементарные исходы должны образовывать полную группу событий, т.е. одно и только одно из них должно произойти в результате реализации испытания;

в) они должны быть равновозможны, исходя из симметрии исходов испытания;

г) количество элементарных исходов n (их нужно найти!) должно быть конечным.

Только при выполнении всех этих условий для расчета вероятности случайного события можно пользоваться классическим определением.

3. В-третьих, необходимо определить элементарные исходы, благоприятные случайному событию А, т.е. такие, при реализации которых А происходит. Число благоприятных исходов m (как в прочем и n) часто находится с помощью формул комбинаторики.

4. И, наконец, согласно классическому определению вероятность случайного события А - P(A) определится как отношение числа исходов, благоприятствующих этому событию m, к общему числу элементарных исходов n:

P(A) = .

Пример 5.12. Какова вероятность выигрыша в лотерее 5 из 36 (для выигрыша необходимо совпадение всех 5 чисел)?

Решение. Испытание состоит в случайном выборе 5 чисел из 36 возможных. Элементарные исходы испытания – это всевозможные наборы 5 чисел, различающиеся только по составу и не различающиеся по расположению чисел, так как порядок выпадения чисел не имеет значения. Примеры элементарных исходов: 1,2,3,4,5; 1,2,3,4,6 и т.д. Из случайности выбора очевидно, что такие исходы – равновозможны. Общее количество элементарных исходов, образующих полную группу событий как всевозможных вариантов розыгрыша 5 чисел из 36, равно числу сочетаний из 36 по 5, т.е. n= 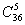. Число благоприятных вариантов для выигрыша (совпадение всех 5 чисел) равно одному: m =1 – только на одну комбинацию чисел приходится полный выигрыш. Таким образом, вероятность выигрыша в этой лотерее

.

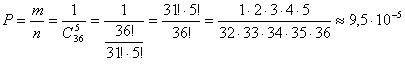Пример 5.13. Какова вероятность того, что номер случайно выбранной автомашины не содержит одинаковых цифр?

Решение. Здесь испытание состоит в выборе случайным образом номера автомобиля, состоящего из трех цифр (мы не рассматриваем буквенные отличия номеров). Элементарные события – всевозможные номера (трехзначные числа, начиная от 001 и заканчивая 999). Полное количество элементарных исходов испытания – количество всех номеров – n= 999.

В примере 5.10 мы нашли количество номеров автомашин, цифры которых не повторялись. Для нашего примера это число – количество благоприятных исходов m искомого случайного события А. m = 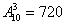. Значит, вероятность того, что номер случайно выбранной автомашины не будет содержать одинаковых цифр

.

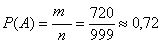Пример 5.14. К урсант выучил 40 экзаменационных вопросов из 60. Каждый билет состоит из двух вопросов, распределенных случайным образом. Найдите вероятность того, что курсант знает а) оба вопроса из вытащенного наугад билета; б) хотя бы один вопрос.

Решение. Рассмотрим испытание, состоящее в выборе билета, т.е. двух вопросов из 60. Общее количество исходов такого испытания равно числу сочетаний (порядок вопросов в билете несущественен) из 60 по 2. Они равновозможны, образуют полную группу событий и число их конечно n= 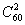. По формуле (5.3) n= 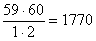. Значит, испытание сводится к схеме случаев и можно пользоваться классическим определением вероятности. Количество благоприятных исходов события А – курсант знает оба вопроса из доставшихся – определяется числом сочетаний из 40 по 2. 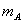= 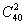. Вычисляем 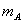по той же формуле: 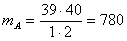. Подставляя найденные 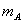и n в формулу (5.1), получим искомую вероятность .

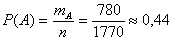Найдем вероятность события В – курсант знает хотя бы один вопрос из двух доставшихся. Множество благоприятных исходов данного события состоит из множества благоприятных исходов события А (курсант знает оба вопроса в билете) и множества исходов, при которых курсант знает один вопрос, а другой – нет. Число таких исходов равно произведению числа выученных вопросов (способы выбора первого вопроса) на число не выученных вопросов (способы выбора второй вопрос), т.е. 40 20=800. Таким образом, 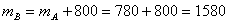. И вероятность события В:

.

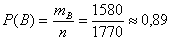Пример 5.15. Бросаются две игральные кости. Найти вероятность того, что сумма выпавших очков равна 8.

Решение. Испытание состоит в броске двух костей (идеальных кубиков). Элементарным событием будет упорядоченная пара целых чисел от 1 до 6. Например, (1,4), что означает выпадение единицы на первой кости и четверки – на второй. Все элементарные исходы можно представить в следующей таблице:

.

Число элементарных исходов равно 36. Так как броски никак не зависят друг от друга, то элементарные исходы – равновозможны.

Обозначим случайное событие А – получение в сумме 8 очков. Благоприятные исходы этого события: (2,6), (3,5), (4,4), (5,3), (6,2). Всего 5 исходов. Значит, вероятность того, что в сумме на двух игральных костях выпадет восемь очков, равна:

.

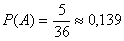Пример 5.16. Задача ландскнехта! Однажды к Галилею за консультацией обратился ландскнехт. Его интересовал вопрос: что вероятнее при броске трех игральных костей – получить в сумме 11 или 12. Он заявил, что согласно логике обе эти суммы должны выпадать одинаково часто, но на опыте (а ландскнехт проделал его несколько тысяч раз) сумма 11 выпадала чаще 12.

В качестве элементарных событий испытания, состоящего в бросании трех костей и подсчитывании при этом суммы всех очков, ландскнехт взял варианты разложения получающейся суммы. Так, и 11, и 12 в сумме можно получить шестью различными способами:

11=1+4+6=1+5+5=2+3+6=2+4+5=3+3+5=3+4+4,

12=1+5+6=2+4+6=2+5+5=3+4+5=3+3+6=4+4+4.

Отсюда, по его мнению, и вытекает равная вероятность выпадения этих сумм.

Однако Галилей нашел ошибку в его рассуждениях. Оказывается, варианты разложения сумм нельзя брать в качестве элементарных событий в таком виде, как это делал ландскнехт, потому что они не равновозможны. Действительно, разложение 4+4+4 может быть получено единственным образом, когда четверка выпадает на всех трех костях. Разложение 1+5+5 может быть получено уже тремя различными способами: 1+5+5=5+1+5=5+5+1, когда единица выпадает на первой, либо на второй, либо на третьей кости, а на других – пятерки. А разложение 1+4+6 можно представить шестью различными вариантами: 1+4+6 = 1+6+4 = 4+1+6 = 4+ 6+1= 6+1+4 = 6+4+1. Здесь, к примеру, сумма 1+4+6 означает, что единица выпала на первой кости, четверка - на второй, а шестерка – на третьей. Таким образом, общая сумма в 11 очков может быть получена 27 различными способами, а 12 - только 25 способами. В качестве элементарного события необходимо брать упорядоченную тройку целых чисел, каждое из которых изменяется от 1 до 6, например (1, 2, 5). Общее количество элементарных исходов подсчитывается из правила произведения: 6×6×6= 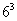=216. И, согласно классическому определению, вероятность выпадения суммы в 11 очков 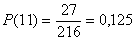, а суммы в 12 очков - 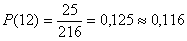. Эти события имеют разную вероятность, хотя разность вероятностей составляет всего 0,009.

В рассмотренных задачах для использования классического определения вероятности в расчетах необходимо выполнение следующих условий:

1) число элементарных событий, образующих полную группу, должно быть конечным;

2) данные элементарные события должны быть равновозможны.

Если не выполнено хотя бы одно из двух условий, классическое определение не применимо. На практике существует много экспериментов, элементарные события которых не удовлетворяют первому или второму условию. Следовательно, для них нельзя находить вероятности случайных событий, пользуясь классическим определением. Однако существуют другие определения вероятности, не обладающие рассмотренными недостатками.

Иногда недостаток конечного числа возможных исходов испытания можно преодолеть, используя геометрическое определение вероятности.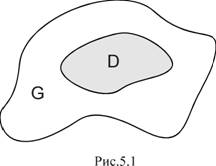

Рассмотрим некоторую замкнутую область G в пространстве (рис.5.1). Обозначим через 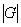ее меру. Если область – одномерная (отрезок), то мерой будет ее длина, если область двумерная (некоторая плоская фигура), то ее мера - площадь, если трехмерная (тело в пространстве), то – объем. Пусть область D полностью содержится в области G. Мера области D - .

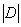Рассмотрим следующий эксперимент: случайно из области G выбирается точка А. Необходимо определить вероятность попадания точки А в подобласть D.

Роль элементарных событий в данном эксперименте играют точки области G. Все множество точек области G образует пространство элементарных событий. Все элементарные события – равновозможны, так как все точки области G равноправны в отношении попадания туда случайной точки A. Но число этих элементарных событий бесконечно. Поэтому в данном случае классическое определение вероятности не применимо.

Согласно геометрическому определению,

вероятность случайного события А равна отношению меры области, благоприятствующей появлению события А, к мере всей области, т.е.

.

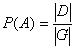Пример 5.17. Задача о встрече. Двое лиц договариваются о встрече на следующих условиях: каждый из них приходит к указанному месту независимо друг от друга в любой момент времени от двенадцати до часу и ждет другого в течение 20 минут, после чего уходит. Какова вероятность того, что встреча состоится?

Решение. Обозначим через x и y моменты прихода к месту встречи 1-го и 2-го лица. Изобразим момент встречи в декартовой системе координат Oxy: за начало координат возьмем 12 ч., а за единицу измерения – 1ч. Элементарное событие исхода встречи – упорядоченная пара чисел (x, y) – обозначается на плоскости точкой. Так как по условию задачи встречающиеся должны прийти к назначенному месту в течение часа, то 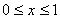, 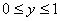и множество всех элементарных событий G образует на плоскости квадрат со стороной 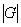1. =1.

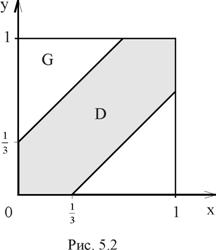Встреча произойдет тогда и только тогда, если разность между x и y будет меньше либо равна 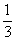ч., т.е. если 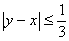. Этим неравенством и определяется подобласть D.

Изобразим на графике (рис.5.2) границы подобласти D: y - x = 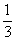и y - x = 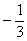; y= x + 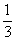и y= x .

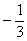Найдем площадь области D.

= .

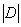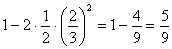По геометрическому определению вероятность встречи = .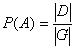

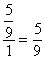Существует большой класс событий, которые могут появиться в результате испытаний, не обладающих симметрией возможных исходов. Так, например, из соображений симметрии невозможно определить вероятность раскрытия какого-либо типа преступления конкретным следователем или вероятность рождения определенного количества мальчиков в год. В этих случаях вероятность случайного события можно определить исходя из того, насколько часто данное событие будет появляться в однотипных испытаниях.

Если производится серия из n испытаний, в каждом из которых может появиться (или не появиться) случайное событие А, то отношение числа испытаний, в которых появилось событие А - m, к общему числу испытаний n называют статистической вероятностью события А в данной серии испытаний .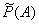

Итак, статистическая вероятность случайного события А равна относительной частоте появления этого события в ряде испытаний, т.е.

,

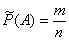где m – число испытаний, в которых появилось событие А;

n – общее число испытаний.

Это и есть статистическое определение вероятности.

В отличие от вероятности 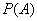, рассматриваемой в классическом определении, статистическая вероятность 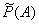- величина опытная, полученная в результате эксперимента. 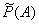в значительной мере имеет случайный характер.

Рассмотрим испытание, состоящее в бросании плоской монеты, и событие А – выпадение герба. Классическая вероятность этого события 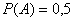. Что касается статистической вероятности события 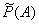, то она зависит от числа произведенных испытаний в серии и может не равняться 0,5. Скажем, если общее число испытаний n будет нечетным, то число выпавших гербов всегда будет не равно числу «решек» и 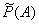будет отличаться от 0,5. Однако для дальнейшего использования статистической вероятности важно насколько она отличается от полученной из классического определения. Произведем серию из 60 испытаний, каждый раз подсчитывая статистическую вероятность выпадения герба.

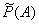
Появление герба - 1, решки - 0	Число выпавших гербов	Число испыта-ний	Статистическая вероятность	Появление герба - 1, решки - 0	Число выпавших гербов	Число испытаний	Статистическая вероятность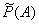
			1,0000				0,5161
			0,5000				0,5000
			0,6667				0,4848
			0,7500				0,5000
			0,6000				0,5143
			0,5000				0,5000
			0,5714				0,5135
			0,6250				0,5000
			0,5556				0,5128
			0,6000				0,5000
			0,6364				0,5122
			0,5833				0,5238
			0,6154				0,5116
			0,5714				0,5000
			0,5333				0,5111
			0,5625				0,5217
			0,5294				0,5106
			0,5000				0,5208
			0,5263				0,5102
			0,5500				0,5000
			0,5238				0,5098
			0,5000				0,5000
			0,5217				0,5094
			0,5417				0,5000
			0,5200				0,4909
			0,5000				0,5000
			0,5185				0,5088
			0,5000				0,5000
			0,5172				0,4915
			0,5333				0,5000

Если количество произведенных испытаний n мало, например, произведено три бросания, то герб может не появиться один раз, т.е. 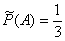, вообще ни разу - 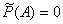или все три раза 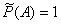. Т.о. статистическая вероятность не будет совпадать со значением, полученным из классического определения, и будет вести себя случайным образом. Из таблицы видно, что при небольшом числе опытов (n <10) относительная частота выпадения герба заметно отличается от классической вероятности. При n =10 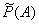=0,60; при n =20 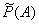=0,55; при n =30 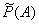=0,5333. При очень большом числе опытов статистическая частота выпадения герба приближается к значению классической вероятности 0,5, колеблясь вокруг этой величины. Причем, чем больше n, тем меньше разность 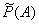- 0,5. Колебания частоты около этого значения носят случайный характер.

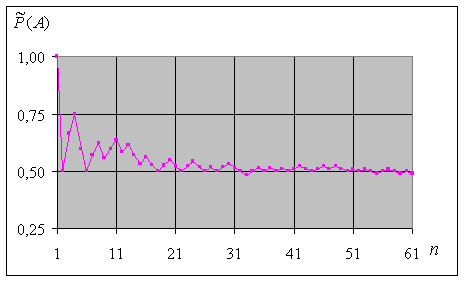
Рис.5.3

На рис.5.3 приведен график зависимости относительной частоты появления герба при бросании монеты 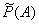от числа опытов n. Из графика видно, что по мере увеличения n частота стабилизируется, стремясь к постоянной величине, которую мы полагаем равной 0,5. Это значение и есть вероятность выпадения герба в одном опыте, подсчитанная при помощи классического определения.

На данном примере, сводящемся к схеме случаев, мы показали, что при достаточно большом количестве опытов относительную частоту события можно принять за приближенное значение его вероятности. Естественно допустить, что и для опытов, не сводящихся к схеме случаев, постоянное значение, к которому при увеличении числа испытаний приближается относительная частота события и есть вероятность этого события.

Здесь возникает вопрос: к любым ли событиям с неопределенным исходом, которые в житейской практике считаются случайными, применимо статистическое определение вероятности? Оказывается, для расчета вероятности по статистическому определению необходимо, чтобы случайное событие обладало рядом свойств.

1. Рассматриваемые события должны быть исходами испытания, которые можно повторить неограниченное число раз. Напомним, что испытание мы определили как совокупность условий, при которых происходит или не происходит случайное событие. Таким образом, для использования статистического определения необходимо, чтобы комплекс условий, при которых реализуется случайное событие, был идентичен и его можно было повторить неограниченное число раз. Поэтому бессмысленно ставить вопрос об определении вероятности, например, возникновения войны или совершения преступления, поскольку данные события возникают при уникальных, неповторимых условиях.

2. Число испытаний, в результате которых появляется событие А, должно быть достаточно велико.

3. События должны обладать статистической устойчивостью. Это означает, что в различных сериях испытаний относительная частота должна изменяться незначительно, колеблясь около постоянного числа. Это число и является вероятностью случайного события.

Дата добавления: 2014-01-07