Индукционный измерительный механизм

Принцип действия этого механизма заключается во взаимодействии двух или более переменных магнитных потоков с индуктированными ими токами в подвижной части (например, алюминиевый диск). Рассмотрим возникновение вращающего момента на примере трехпоточного индукционного механизма, схема которого приведена на рис. 3.5.

Индукционный тангенциальный трехпоточный механизм представляет собой сочетание двух электромагнитов 1 и 2 с воздушными зазорами в сердечниках и обмотками, по которым протекают токи I ₁ и I ₂ , несовпадающие по фазе.

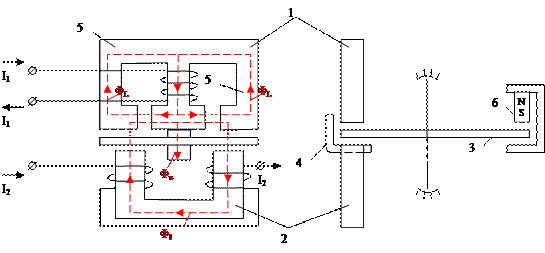
Рис.3.5. Схема тангенциального индукционного механизма.

Током I ₁ создается два магнитных потока: Ф _u – рабочий поток, пересекающий диск и замыкающийся через противополюс 4, и поток Ф _L – нерабочий (диск он не пересекает и замыкается через боковые стержни 5). Током I ₂ создается магнитный поток Ф_I, который в двух местах пересекает диск и замыкается через сердечник 1. Поток Ф_I один, но так как он в двух местах пересекает диск, то можно считать, что диск пересекается двумя потоками со сдвигом 180^о. При этом диск, помещенный в междуполюсное пространство, пересекают три потока, сдвинутые относительно друг друга в пространстве и по фазе:

Ф _u, Ф_I, - Ф_I. Эти потоки образуют в межполюсном пространстве бегущее магнитное поле, пересекающее диск, в результате чего последний начинает вращаться. Ускорение создается при постоянном магните 6, между полюсами которого вращается диск.

Используя упрощенную векторную диаграмму, приведенную на рис. 3.6, покажем получение выражения для вращающего момента в индукционном механизме.

Рис. 3.6. Векторные диаграммы потоков, токов в диске индукционного механизма

Пусть 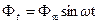– поток, а 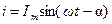– вихревой ток в диске со сдвигом по фазе на угол a по отношению к потоку. Мгновенный вращающий момент при этом будет равен 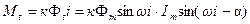, где к – коэффициент пропорциональности.

Из-за инерции диска он будет перемещаться под действием среднего вращающего момента за период

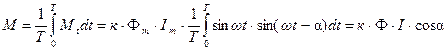. (3.9)

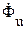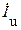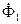С учетом выражения 3.9. из векторных диаграмм (рис. 3.6) видно, что вращающие моменты от взаимодействия и ; и будут равны нулю (углы между этими парами векторов равны 90^о).

Вращающий момент от взаимодействия 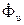и будет равен

, (3.10)

где I _I – вихревой ток в диске, равный ;

- сопротивление диска активное;

r – удельное сопротивление диска;

d – толщина диска.

Индуктивным сопротивлением диска пренебрегаем.

Аналогично вращающий момент от взаимодействия 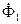и 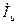будет равен:

, (3.11)

где .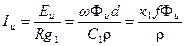

Здесь оба момента действуют в одну сторону и результирующий момент равен алгебраической сумме обоих моментов.

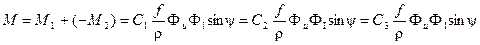(3.12)

Знаки + и – в выражениях 3.10 и 3.11 означают, что в одном случае диск втягивается, а в другой вытягивается.

Дата добавления: 2014-01-07