Уравнение касательной

Иммунный ответ и другие факторы защиты хозяина

При вирусной инфекции, кроме гуморального и клеточного специфического иммунного ответа, действует ряд других факторов защиты хозяина, контролирующих развитие, ограничение и подавление болезни отражается непосредственно в способности макрофагов служить в качестве пермиссивных клеток для репликации вируса ин витро. Многие вирусы, не вызывающие заболевания у старых животных, могут вызывать тяжелую болезнь у новорожденных. Аналогичным образом определяется возрастом хозяина вирулентность некоторых штаммов вируса кори для ЦНС у мышей. Указанные исследования позволяют также предположить, что макрофаги играют важную роль в защите хозяина от вирусной инфекции, а также влияют на зависимые от возраста изменения в чувствительности к вирусным инфекциям.

Роль интерферона в защите хозяина от вирусных инфекций не вполне ясна. Интерферон может действовать непосредствен­но на зараженные вирусом клетки и угнетать продукцию вируса или же активировать противовирусную активность естественных киллерных клеток Во время вирусной инфекции активируются как гумораль­ный, так и клеточный отделы иммунной системы. Однако, для большинства вирусных инфекций нет пока единой точки зрения относительно специфической роли каждого из компонентов иммунной системы в защите и выздоровлении хозяина. Экспрессия вирусных антигенов на по­верхности клеток, зараженных как вирусами с оболочкой, так и вирусами без оболочки служит для инициации иммун­ного ответа и для формирования антигенов-мишеней, распозна­ваемых антителами и иммунными клетками Определенные вирусные белки распознаются иммунной системой и обус­ловливают специфичность иммунного ответа, а также регулиру­ют активацию специфических функциональных частей иммунной системы. В случае реовирусов типоспецифические нейтрализую­щие антитела и типоспецифические цитолитические Т-лим-фоциты так же как и лимфоциты, осуществляющие реакцию гиперчувствительности замедленного типа на­правлены против белка 01 — вирусного гемагглютинина, продук­та гена 51 Один и тот же домен этого полипептида, как опреде­лено с помощью моноклональных антител, распознается и ней­трализующими антителами, и ЦТЛ.

у

f(x)

f(x₀ +Dx) P

Df

f(x₀) M

a b Dx

0 x₀ x₀ + Dx x

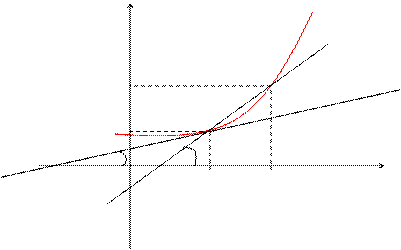
Пусть f(x) определена на некотором промежутке (a, b). Тогда тангенс угла наклона секущей МР к графику функции.

,

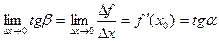где a - угол наклона касательной к графику функции f(x) в точке (x₀, f(x₀)).

Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой: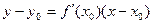

Уравнение нормали к кривой: .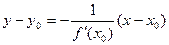

Производная обратных функций

Пусть требуется найти производную функции у = f(x) при условии, что обратная ей функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.

Для решения этой задачи дифференцируем функцию x = g(y) по х:

т.к. g¢(y) ¹ 0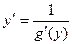

т.е. производная обратной функции обратна по величине производной данной функции.

Пример. Найти формулу для производной функции arctg х.

Функция arctg является функцией, обратной функции tg, т.е. ее производная может быть найдена следующим образом:

Известно, что

По приведенной выше формуле получаем:

Т.к. то можно записать окончательную формулу для производной арктангенса:

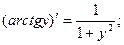
Таким образом получены все формулы для производных арксинуса, арккосинуса и других обратных функций, приведенных в таблице производных.

Дата добавления: 2014-01-07