Фазовый портрет автономной линейной системы второго порядка

ПОПУЛЯЦИОННАЯ МОДЕЛЬ

«ХИЩНИК – ЖЕРТВА»

Рассмотрим систему

. (1)

Положение равновесие:

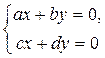
Если

,

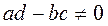точка (0;0) - единственная точка покоя системы.

Фазовые траектории определяются из уравнения

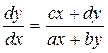(2)

Преобразуем последнее уравнение при помощи линейной неособенной подстановки

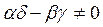, причем (3)

так, чтобы в новых переменных система имела наиболее простой вид.

Из аналитической геометрии известно, что вид уравнения (2) в новых переменных зависит от корней характеристического уравнения системы (1), т.е.

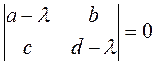(4)

Корни (4) называются собственными числами системы (1).

Анри Пуанкаре показал, что возможны следующие случаи, каждому из которых отвечает свое расположение фазовых кривых в окрестности точки покоя.

I. .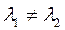

Система (1) приводится к виду

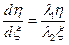(5)

Различают четыре случая.

1) 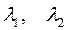- вещественные одного знака.

Точка покоя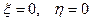называется узлом.

Вид фазовых траекторий:

устойчивый узел неустойчивый узел

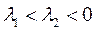
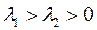
Пример.

Характеристическое уравнение (4) имеет вид:

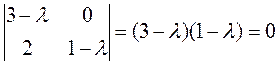
имеет корни 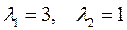. Точка покоя – неустойчивый узел.

2) 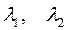- вещественные и противоположных знаков.

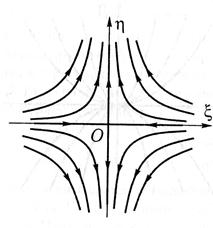
Точка покоя - седло. (неустойчивая точка покоя)

3) 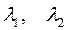- комплексно сопряженные: 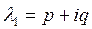, , 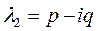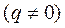. Выделяем вещественные и мнимые части:

.

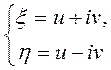Точка покоя - фокус.

устойчивый фокус неустойчивый фокус

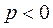
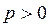
Пример.

Характеристическое уравнение (4) имеет вид:

.

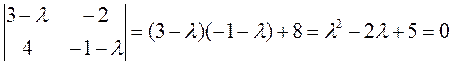имеет дискриминант 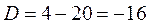, откуда . Точка покоя – неустойчивый узел.

4) 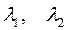- чисто мнимые: 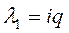, 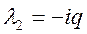. Тогда фазовые траектории – окружности. Точка покоя - центр. (устойчивая точка покоя)

II. Корни характеристического уравнения кратные.

1) Кратные корни не равные нулю, причем .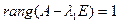

Точка покоя - вырожденный узел.

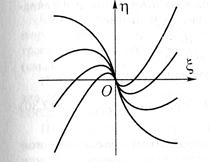
2) Кратные корни не равные нулю, причем .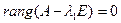

Точка покоя – дикритический узел.

Дата добавления: 2014-01-07