Элементы орбит планет. Основные задачи теоретической астрономии

Движение планеты будет вполне определено, если известны плоскость, в которой лежит ее орбита, размеры и форма этой орбиты, ее ориентировка в плоскости и, наконец, момент времени, в который планета находится в определенной точке орбиты. Величины, определяющие орбиты планеты, называются элементами ее орбиты.

За основную плоскость, относительно которой определяется положение орбиты, принимается плоскость эклиптики.

Две точки, в которых орбита планеты пересекается с плоскостью эклиптики, называются узлами — восходящим и нисходящим. Восходящий узел тот, в котором планета пересекает эклиптику, удаляясь от ее южного полюса.

Эллиптическую орбиту планеты определяют следующие 6 элементов (рис. 28):

1. Наклонение i плоскости орбиты к плоскости эклиптики. Наклонение может иметь любые значения между 0 и 180°. Если 0 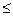i < 90°, то планета движется вокруг Солнца (С) в том же направлении, что и Земля (прямое движение); если 90° < i < 180°, то планета движется в противоположном направлении (обратное движение).

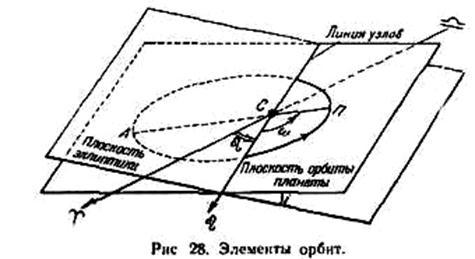
2. Долгота (гелиоцентрическая) восходящего узла 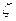, т.е. угол между направлениями из центра Солнца на восходящий узел и на точку весеннего равноденствия. Долгота восходящего узла может иметь любые значения от 0 до 360°.

Долгота восходящего узла 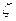и наклонение i определяют положение плоскости орбиты в пространстве.

3. Угловое расстояние 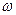перигелия от узла, т.е. угол между направлениями из центра Солнца на восходящий узел 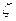, и на перигелий П. Он отсчитывается в плоскости орбиты планеты в направлении ее движения и может иметь любые значения от 0 до 360°.

Угловое расстояние перигелия 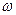определяет положение орбиты в ее плоскости.

4. Большая полуось эллиптической орбиты, которая однозначно определяет сидерический период обращения Т планеты.

5. Эксцентриситет орбиты 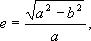где а и b — полуоси эллиптической орбиты.

Большая полуось и эксцентриситет е определяют размеры и форму орбиты.

6. Момент прохождения через перигелий t₀, или положение планеты на орбите в какой-нибудь определенный момент времени t.

Зная момент прохождения через перигелий t₀ и другие элементы орбиты, можно определить положение планеты в плоскости ее орбиты для любого момента времени t.

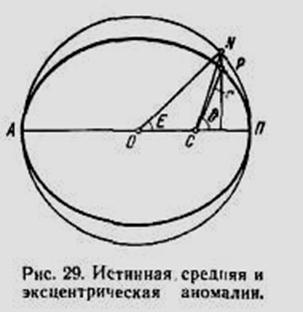
Положение планеты на орбите определяется двумя величинами: радиусом-вектором r и истинной аномалией q. Истинной аномалией планеты называется угол ПСР (рис. 29) между направлением из Солнца (С) на перигелий П и радиусом-вектором планеты Р. Радиус-вектор r и истинная аномалия q вычисляются по формулам

r = a (1 — e cos E), (2.9)

(2.10)

где Е = 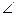ПON и называется эксцентрической аномалией.

Эксцентрическая аномалия Е вычисляется из уравнения Кеплера

M = E — e sin E, (2.11)

где М — угол, называемый средней аномалией. Средняя аномалия представляет собой дугу круга, которую описала бы планета за время (t—t₀), если бы она двигалась равномерно по окружности радиуса а со средней угловой скоростью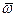, т.е.

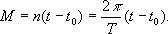(2.12)

Вычисление положения планеты на орбите для некоторого момента времени t проводится в следующей последовательности:

1) по формуле (2.12), в которой известны Т и (t — t₀), определяют среднюю аномалию М;

2) по формуле (2.11), при известных е и М, методом последовательных приближений находят эксцентрическую аномалию Е;

3) по формулам (2.9) и (2.10) вычисляют радиус-вектор r и истинную аномалию q.

Определив положение планеты на орбите для заданных моментов времени, можно вычислить для этих же моментов ее пространственные гелиоцентрические координаты. Зная же элементы орбиты Земли и вычислив для тех же моментов положение Земли на ее орбите, можно определить геоцентрические координаты планеты и найти ее расстояние от центра Земли.

Определение видимых координат планеты по элементам их орбит называется вычислением эфемерид, т.е. таблиц, в которых положения планет даются на любые избранные моменты времени (иногда на много лет вперед).

Обратная задача, т.е. определение элементов орбит по наблюденным координатам, называется определением орбит. Вычисление эфемерид и определение орбит — основные задачи теоретической астрономии.

Дата добавления: 2014-01-07