Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения

Дифференциальное уравнение гармонических колебаний и его решение

Продифференцируем по времени уравнение гармонических колебаний

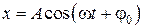. (5.3.1)

и получим выражение для скорости

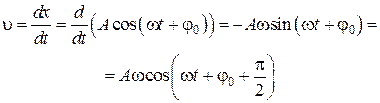. (5.3.2)

Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на p/2. Амплитуда скорости равна А w.

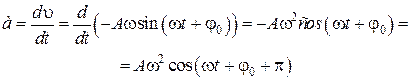. (5.3.3)

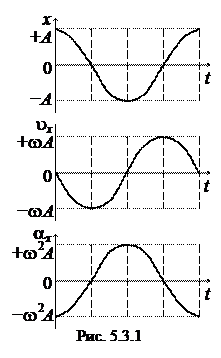Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна А w² (рис. 5.3.1).

Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний

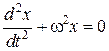, (5.3.4)

где .

Результирующая сила, действующая на материальную точку массой m, определяется с помощью второго закона Ньютона. Проекция этой силы

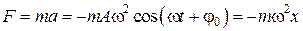. (5.3.5)

Эта сила пропорциональна смещению точки из положения равновесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой. Таким образом, гармонические колебания происходят под действием силы F, пропорциональной смещению x и направленной к положению равновесия,

F = − kx, (5.3.6)

где k = m w² − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая зависимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости (5.3.6) называются квазиупругими силами.

Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором. Ее динамическое поведение описывается дифференциальным уравнением

Þ 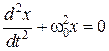, (5.3.7)

w₀ − собственная частота осциллятора.

Решение этого уравнения дает закон движения линейного осциллятора .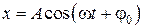

Дата добавления: 2014-01-07