Определение 1. Понятие линейных дифференциальных связей

Понятие линейных дифференциальных связей

Линейные дифференциальные связи первого порядка и условия их интегрируемости

1º. Линейные дифференциальные связи первого порядка и их приведение к дифференциальным уравнениям
в полных дифференциалах

Уравнения связей вида

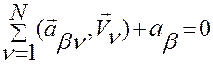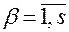, , (2.3.1)

называются линейнымидифференциальными связями.

Здесь векторы 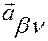и скалярные функции 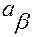, , 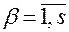зависящие от векторов 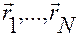, и времени 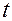, являются непрерывно дифференцируемыми функциями компонент 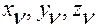, , 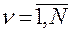и времени .

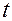В скалярной форме уравнения линейных дифференциальных связей записываются так:

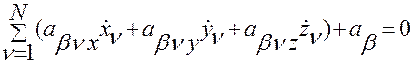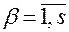, . (2.3.2)

Перейдем к матричной записи этих уравнений.

Введем обозначения:

, , ,…, , , ,

;

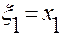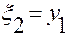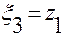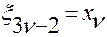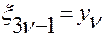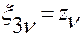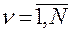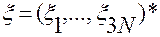— вектор-столбец размерности;

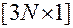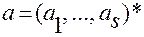— вектор-столбец размерности ;

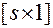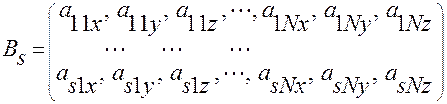; (2.3.3)

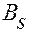— матрица размерности 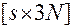, составленная из коэффициентов при 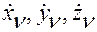уравнений (2.3.2):

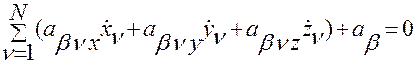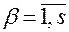, . (2.3.2)

Тогда система (2.3.2) примет вид:

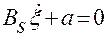. (2.3.2')

На матрицу (2.3.3) накладываем следующие условия:

1) матрица 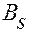и вектор 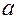непрерывно дифференцируемы по компонентам вектора 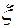и по времени ;

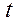2) 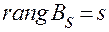, т.е. строки матрицы 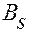линейно независимы при любых .

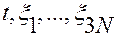1.2.Приведение к системе уравнений
в полных дифференциалах

Умножим на 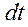каждое уравнение системы (2.3.2'):

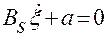. (2.3.2')

Получим систему

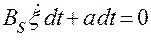. (2.3.2'')

Учтем, что на движениях механической системы

,

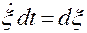и введем обозначения:

, , ;

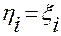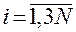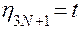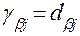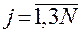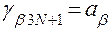при , при ;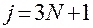

.

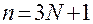Здесь:

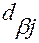— элемент матрицы 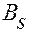под номером ,

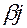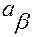— элемент вектора ;

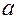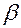— номер уравнения в системе (2.3.2');
принимает значения .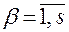

Присоединим к матрице 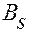столбец 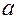. Новую матрицу обозначим .

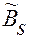Тогда в скалярной форме система уравнений (2.3.2''):

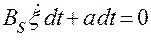(2.3.2'')

примет вид

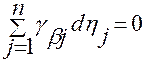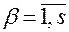, . (2.3.4)

Здесь:

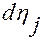— дифференциал функции ;

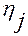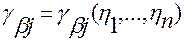— функции, непрерывно дифференцируемые по всем аргументам.

На уравнения (2.3.4) можно смотреть как на уравнения в полных дифференциалах (или точных дифференциалах), которые должны выполняться при любых значениях 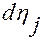вдоль движений механической системы, удовлетворяющих уравнениям связей.

2º.Понятие уравнений в полных дифференциалах

В общем случае под системой уравнений в полных дифференциалах понимается следующая система уравнений

, , .

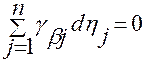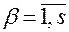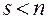В ней:

– коэффициенты 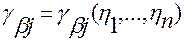– функции, заданные и непрерывно дифференцируемые по совокупности аргументов при всех значениях ;

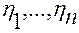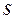– переменных 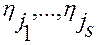среди аргументов 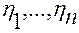– являются функциями, зависящими от остальных переменных , , ;

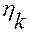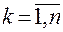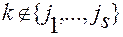– функции 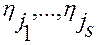– предполагаются непрерывно дифференцируемыми по своим аргументам;

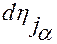– – дифференциал функции , ;

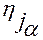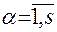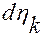– – дифференциал переменной ,

, ;

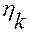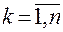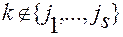– если обозначим матрицу коэффициентов 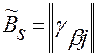, , 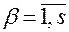, 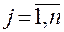то для нее выполняется условие:

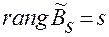
при любых значениях .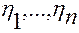

Такая система уравнений называется системой уравнений в полных дифференциалах.

3º. Условия интегрируемости уравнения
в полных дифференциалах в случае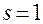
(одна дифференциальная связь)

3.1.Одна дифференциальная связь. Понятие
интегрируемости и полной интегрируемости

3.1.1.Уравнение в полных дифференциалах
для одной дифференциальной связи

В случае 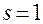уравнение в полных дифференциалах имеет вид:

. (2.3.5)

Здесь

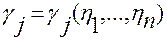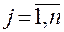· , — функции, заданные при 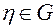и непрерывно дифференцируемые по переменным ;

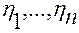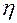· обозначает вектор размерности 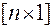, компонентами которого являются переменные ;

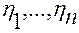· область 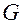— открытое связное множество.

Из условия, накладываемого на матрицу коэффициентов

,

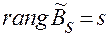вытекает, что для любой точки 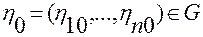существует такой коэффициент 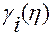, что

.

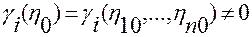В силу непрерывности функции 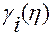это неравенство справедливо, по крайней мере, в некоторой окрестности точки 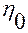, содержащейся в области .

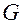Введем следующие обозначения.

Если какая-либо функция 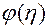не зависит явно от переменной 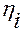из совокупности 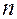переменных 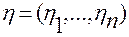, то совокупность переменных 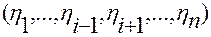будем обозначать 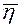, а функцию 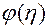, соответственно, .

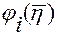3.1.2. Понятие интегрируемости уравнения
в полных дифференциалах

Дадим понятие интегрируемости уравнения (2.3.5) и определение решения уравнения (2.3.5):

. (2.3.5)

Дата добавления: 2014-01-07