Необходимость

Дополнение 4 к п.3 (к стр. 13 лекции)

Достаточность

Доказательство достаточности можно найти в монографии Ф.Хартман. «Обыкновенные дифференциальные уравнения», Мир, М., 1970, в главе 6 (стр.144-163).

Пример. Движение конька

На рисунке 2.3.1 конек схематично представлен в виде отрезка 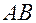, положение которого зафиксировано в некоторый момент времени 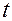в плоскости 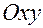его движения.

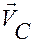
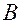
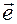
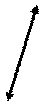
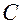
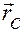
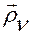
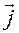
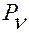
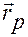
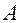
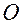
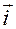
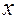
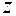
Рис.2.3.1

Движение конька рассматриваем в системе отсчета с направляющими ортами .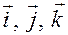

Обозначим 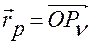— радиус-вектор любой точки 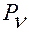лезвия конька, а 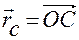— радиус-вектор некоторой фиксированной точки 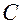этого лезвия.

На рис.2.3.1 в качестве точки 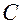выбрана середина лезвия конька.

Обозначим 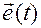— направляющий орт прямой 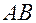, на которой в момент времени 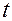находится лезвие конька. Направляющий вектор этой прямой совпадает с направлением стопы фигуриста от пятки к пальцам.

Пусть 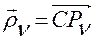. Тогда можем записать

, .

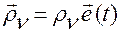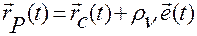Здесь 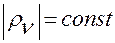— расстояние от точки до точки в любой момент времени .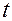

Отсюда следует, что движение любой точки лезвия конька определено, если определены движение 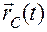точки 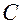и закон изменения направления орта .

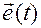Это значит, что для того, чтобы знать движение любой точки лезвия конька, достаточно определить движение 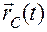точки 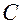и движение орта .

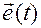Введем следующие обозначения:

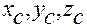– — координаты точки ;

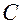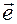– — угол между ортом и плоскостью ,
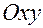отсчитываемый от плоскости 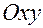до орта ;

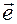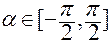, причем, если 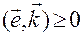, то ;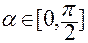
если 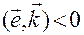, то ;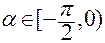

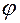– — угол, отсчитываемый от орта 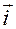оси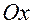

в плоскости 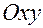до проекции орта 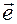на эту плоскость; угол отсчитывается в положительном направлении оси 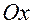относительно орта ; .

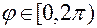В этих обозначениях будем иметь

,

.

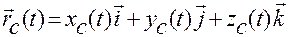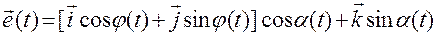Отсюда следует, что для определения движения конька, достаточно знать закон изменения пяти координат: .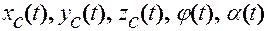

Будем рассматривать следующую модель движения конька.

1. Движение лезвия при всех 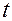происходит в плоскости 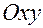(конек не отрывается от плоскости льда).

2. Точка 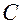движется так, что ее скорость 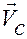остается параллельной орту .

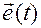Из условия 1 вытекает, что в предлагаемой модели движения должны выполняться ограничения, являющиеся голономными стационарными связями:

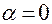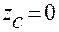; . (2.3.29)

Если обозначить 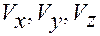компоненты вектора 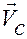в системе , то из второго условия предлагаемой модели движения находим следующие ограничения, которые имеют вид дифференциальных связей первого порядка:

, .

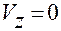Учитывая, что , , 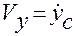, 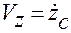от этих уравнений переходим к уравнениям в полных дифференциалах:

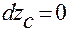, (2.3.30)

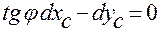. (2.3.31)

Дифференциальная связь (2.3.30) интегрируема. После ее интегрирования придем к геометрической связи (2.3.29). Поэтому связь (2.3.30) можно исключить из рассмотрения.

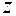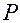Покажем, что связь (2.3.31) неинтегрируемая. Уравнение этой связи по виду совпадает с уравнением (2.3.27), в котором следует заменить обозначение переменной буквой , а коэффициенты и 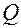заменить функциями

, .

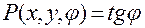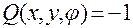Поэтому, применяя следствие 2, можем записать, что необходимое и достаточное условие интегрируемости связи (2.3.31) задается тождеством (2.3.28):

.

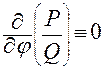Подставляя в левую часть этого тождества явное выражение функци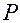й и 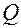, получаем

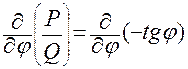0.

Поскольку данное соотношение не является тождеством, то из следствия 2 делаем вывод, что связь (2.3.31) неинтегрируемая.

5. Дополнение 5 к п. 4 §3 (к стр. 20 лекции)

Теорема 4 (вторая теорема Фробениуса)

Для того чтобы система (2.3.35)

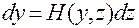(2.3.35)

была вполне интегрируема в области 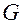, необходимо и достаточно, чтобы выполнялись следующие условия:

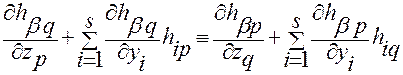(2.3.36)

для всех ;.

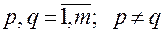Тождества (2.3.36) рассматриваются по всем значениям переменных 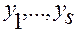, 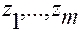в области .

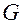Пусть система (2.3.35)

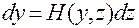. (2.3.35)

вполне интегрируема в области .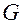

Это значит, что для любых 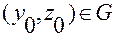существуют функции 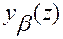, , являющиеся компонентами вектора , со свойствами, указанными в определении 5.

Тогда подстановка функций 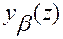в систему (2.3.35) обращает уравнения в тождества.

Из этих тождеств делаем вывод о том, что правые части уравнений (2.3.35) являются полными дифференциалами функций , .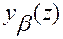

Тогда, согласно теореме 1 из п.3º, для коэффициентов

и ,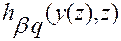

каждого из уравнений с номером 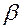, , справедливы тождества:

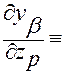
, (2.3.37)

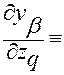
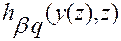, (2.3.38)

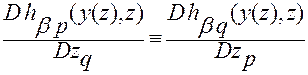(2.3.39)

для всех , для которых определены функции .

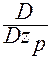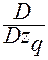Здесь в последнем тождестве через и обозначены операторы вычисления частной производной по координате 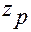и 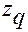, соответственно, от суперпозиции функци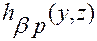й и 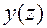(для оператора 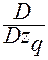) и функци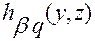й и 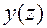(для оператора ).

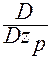Раскроем левую часть тождества (2.3.39). Будем иметь

.

Подставляя в правую часть вместо 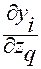тождество (2.3.38), записанное для 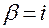, окончательно получим

(2.3.40)

Аналогично, вычисляя правую часть тождества (2.3.39) и учитывая тождество (2.3.37) для 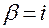, найдем

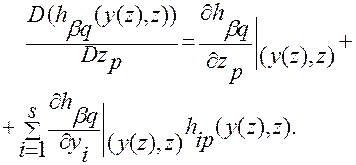(2.3.41)

После подстановки функций (2.3.40) и (2.3.41) в соотношение (2.3.39), оно примет вид:

;.

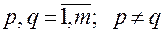Эти тождества справедливы для всех 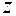, для которых определены функции .

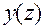Полагая в них 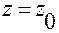и учитывая, что 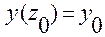, придем к следующим равенствам

;.

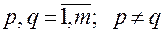В силу произвольности выбора точки 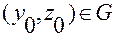, полученные равенства справедливы для всех точек области 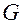. А это значит, что имеют место тождества (2.3.36) по .

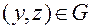Необходимость доказана.

Доказательство достаточности можно найти в монографии:

Ф.Хартман. «Обыкновенные дифференциальные уравнения», Мир, М.,1970, в главе 6 (стр.144 - 163).

Дата добавления: 2014-01-07