Математическая модель системы

Задача построения математической модели ИС может быть поставлена следующим образом: для конкретной цели моделируемой операции с учетом имеющихся ресурсов построить операторы моделирования исхода операции и оценки показателя ее эффективности. Формальная запись этой задачи имеет вид:

,

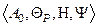где – цель; 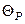– имеющиеся ресурсы; – оператор моделирования исхода операции; – оператор оценки показателя эффективности.

Перед рассмотрением каждого из названных операторов приведем два важных определения.

Оператором в математике называют закон (правило), согласно которому каждому элементу х множества X ставится в соответствие определенный элемент у множества Y. При этом множества X и Y могут иметь самую различную природу (если они представляют, например, множества действительных или комплексных чисел, понятие оператор совпадает с понятием функции).

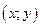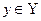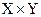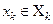Множество Z упорядоченных пар , где , , называется прямым произведением множеств X и Y и обозначается . Аналогично, множество Z упорядоченных конечных последовательностей , где , называется прямым произведением множеств 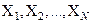и обозначается

.

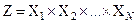Оператором моделирования исхода операции называется оператор Н, устанавливающий соответствие между множеством учитываемых в модели факторов, множеством U возможных стратегий управления системой (операцией) и множеством Y значений выходных характеристик модели

,

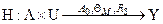где — ресурсы на этапе моделирования исходов операции и учитываемые свойства моделируемой системы соответственно.

Оператором оценки показателя эффективности системы (операции) называется оператор , ставящий в соответствие множеству Y значений выходных характеристик модели множество W значений показателя эффективности системы

,

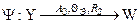где — ресурсы исследователя на этапе оценивания эффективности системы.

Особо отметим, что построение приведенных операторов всегда осуществляется с учетом главного системного принципа – принципа цели. Кроме того, важным является влияние объема имеющихся в распоряжении исследователя ресурсов на вид оператора моделирования исхода Н и состав множества U стратегий управления системой (операцией). Чем больше выделенные ресурсы, тем детальнее (подробнее) может быть модель и тем большее число стратегий управления может быть рассмотрено (из теории принятия решений известно, что первоначально множество возможных альтернатив должно включать как можно больше стратегий, иначе можно упустить наилучшую).

В самом общем виде математической моделью системы (операции) называется множество

,

элементами которого являются рассмотренные выше множества и операторы.

Способы задания оператора и подходы к выбору показателя эффективности W рассматриваются в теории эффективности; методы формирования множества возможных альтернатив – в теории принятия решений.

Для двух классов задач показатель эффективности в явном виде не вычисляется:

· для задач так называемой прямой оценки, в которых в качестве показателей эффективности используются значения одной или нескольких выходных характеристик модели;

· для демонстрационных задач, в ходе решения которых для изучения поведения системы используются лишь значения ее выходных характеристик и внутренних переменных.

В таких случаях используют термин "математическое описание системы", представляемое множеством

.

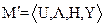Классификация математических моделей

В качестве основного классификационного признака для математических моделей целесообразно использовать свойства операторов моделирования исхода операции и оценки показателя ее эффективности.

Оператор моделирования исхода Н может быть функциональным (заданным системой аналитических функций) или алгоритмическим (содержать математические, логические и логико-лингвистические операции, не приводимые к последовательности аналитических функций). Кроме того, он может быть детерминированным (когда каждому элементу множества 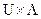соответствует детерминированное подмножество значений выходных характеристик модели 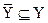) или стохастическим (когда каждому значению множества 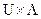соответствует случайное подмножество ).

Оператор оценивания показателя эффективности может задавать либо точечно-точечное преобразование (когда каждой точке множества выходных характеристик Y ставится в соответствие единственное значение показателя эффективности W), либо множественно-точечное преобразование (когда показатель эффективности задается на всем множестве полученных в результате моделирования значений выходных характеристик модели).

В зависимости от свойств названных операторов все математические модели подразделяются на три основных класса:

· аналитические;

· статистические;

· имитационные.

Для аналитических моделей характерна детерминированная функциональная связь между элементами множеств U, , Y, а значение показателя эффективности W определяется с помощью точечно-точечного отображения. Аналитические модели имеют весьма широкое распространение. Они хорошо описывают качественный характер (основные тенденции) поведения исследуемых систем. В силу простоты их реализации на ЭВМ и высокой оперативности получения результатов такие модели часто применяются при решении задач синтеза систем, а также при оптимизации вариантов применения в различных операциях.

К статистическим относят математические модели систем, у которых связь между элементами множеств U, , Y задается функциональным оператором Н, а оператор является множественно-точечным отображением, содержащим алгоритмы статистической обработки. Такие модели применяются в тех случаях, когда результат операции является случайным, а конечные функциональные зависимости, связывающие статистические характеристики учитываемых в модели случайных факторов с характеристиками исхода операции, отсутствуют. Причинами случайности исхода операции могут быть случайные внешние воздействия; случайные характеристики внутренних процессов; случайный характер реализации стратегий управления. В статистических моделях сначала формируется представительная выборка значений выходных характеристик модели, а затем производится ее статистическая обработка с целью получения значения скалярного или векторного показателя эффективности.

Имитационными называются математические модели систем, у которых оператор моделирования исхода операции задается алгоритмически. Когда этот оператор является стохастическим, а оператор оценивания эффективности задается множественно-точечным отображением, имеем классическую имитационную модель. Если оператор Н является детерминированным, а оператор задает точечно-точечное отображение, можно говорить о вырожденной имитационной модели,

На рис. 2 представлена классификация наиболее часто встречающихся математических моделей по рассмотренному признаку.

Важно отметить, что при создании аналитических и статистических моделей широко используются их гомоморфные свойства (способность одних и тех же математических моделей описывать различные по физической природе процессы и явления). Для имитационных моделей в наибольшей степени характерен изоморфизм процессов и структур, т.е. взаимно-однозначное соответствие элементов структур и процессов реальной системы элементам ее математического описания и, соответственно, модели.

Основная классификация математических моделей.

Вид основных операторов	H
функциональный	алгоритмический
детермин.	стохастих.	детермин.	стохастих.
	Множественно-точечное отображение		Статистические		Имитационные
Точечно-точечное отображение	Аналитические		Имитационные

Изоморфизм — соответствие (отношение) между объектами, выражающее тождество их структуры (строения). Именно таким образом организовано большее число классических имитационных моделей. Названное свойство имитационных моделей проиллюстрировано рис. 3. На рисунке обозначены: 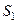— система-оригинал; — изоморфное отображение оригинала; 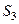— гомоморфное отображение оригинала.

Имитационные модели являются наиболее общими математическими моделями. В силу этого иногда все модели называют имитационными:

· аналитические модели, "имитирующие" только физические законы, на которых основано санкционирование реальной системы, можно рассматривать как имитационные модели I уровня;

· статистические модели, в которых, кроме того, "имитируются" случайные факторы, можно называть имитационными моделями II уровня;

· собственно имитационные модели, в которых еще имитируется и функционирование системы во времени, называют имитационными моделями III уровня.

Рис. 3. Пример изоморфного и гомоморфного отображений.

На рис. 4 представлена классификация моделей (прежде всего аналитических и статистических) по зависимости переменных и параметров от времени. Динамические модели, в которых учитывается изменение времени, подразделяются на стационарные (в которых от времени зависят только входные и выходные характеристики) и нестационарные (в которых от времени могут зависеть либо параметры модели, либо ее структура, либо и то и другое).

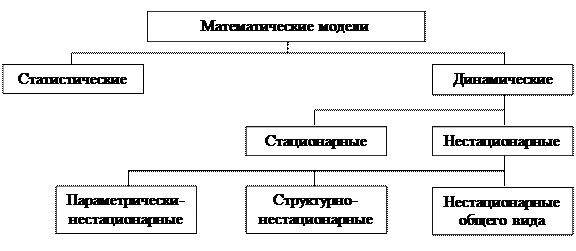
Рис. 4. Классификация математических моделей по зависимости переменных и параметров от времени.

На рис. 5 показана классификация математических моделей еще по трем основаниям: по характеру изменения переменных; по особенностям используемого математического аппарата; по способу учета проявления случайностей.

Названия типов (видов) моделей в каждом классе достаточно понятны. Укажем лишь, что в сигнально-стохастических моделях случайными являются только внешние воздействия на систему.

Имитационные модели, как правило, можно отнести к следующим типам:

· по характеру изменения переменных — к дискретно-непрерывным моделям;

· по математическому аппарату — к моделям смешанного типа;

· по способу учета случайности — к стохастическим моделям общего вида.

Рис. 5. Классификация математических моделей.

Дата добавления: 2014-01-07