
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Адиабатный процесс
|
|
|
|
Существует достаточно много явлений, например, нагревание ручного насоса при накачивании шин, понижение температуры воздуха после извержения вулкана, при котором быстро расширяются газы, изменение температуры воздуха при сильных порывах ветра, процессы, происходящие с веществом, заключённым в теплоизолирующую оболочку, распространение звуковых волн и многие другие, объяснить которые можно, используя понятие адиабатного процесса.
Адиабатный процесс это процесс, происходящей без теплообмена системы с окружающей средой.
Реализовать такой процесс на практике можно, быстро сжимая или расширяя газ, или заключая его в теплоизолирующую оболочку (термос, сосуд Дьюара). При адиабатном процессе 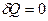 , а, следовательно, первое начало термодинамики будет иметь вид:
, а, следовательно, первое начало термодинамики будет иметь вид:  или
или  . При адиабатном расширении газ совершает механическую работу за счёт убыли собственной внутренней энергии. При адиабатном сжатии внутренняя энергия газа растёт за счёт работы внешних сил, сжимающих его.
. При адиабатном расширении газ совершает механическую работу за счёт убыли собственной внутренней энергии. При адиабатном сжатии внутренняя энергия газа растёт за счёт работы внешних сил, сжимающих его.
Получим уравнение адиабаты, используя первое начало термодинамики. Приращение внутренней энергии можно записать через молярную изохорическую теплоёмкость: 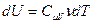 , элементарную работу – через давление и приращение объёма:
, элементарную работу – через давление и приращение объёма:  . Получим
. Получим
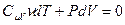 (4.31)
(4.31)
Исключим из этого уравнения приращение температуры, используя уравнение Менделеева - Клапейрона 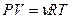 . Продифференцируем его и получим:
. Продифференцируем его и получим: 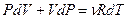 , отсюда выразим приращение температуры
, отсюда выразим приращение температуры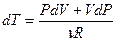 и подставим его в (4.31), после приведения подобных получим:
и подставим его в (4.31), после приведения подобных получим: 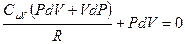 . Заменим в этом равенстве R на
. Заменим в этом равенстве R на  , приведём к одному знаменателю, раскроем скобки и получим:
, приведём к одному знаменателю, раскроем скобки и получим:
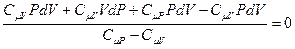 .
.
Так как знаменатель не равен нулю, то равенство будет выполняться, если числитель равен нулю. После приведения подобных получим:
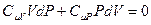 .
.
Обозначим отношение теплоёмкостей  . Это отношение g принято называть показателем адиабаты или коэффициентом Пуассона. После введения g получим:
. Это отношение g принято называть показателем адиабаты или коэффициентом Пуассона. После введения g получим:
 .
.
Поделим обе части равенства на PV и получим уравнение с разделяющимися переменными:  . Проинтегрируем это уравнение и получим:
. Проинтегрируем это уравнение и получим: или
или 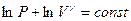 . Воспользуемся свойством логарифмов: сумму логарифмов можно представить как логарифм произведения:
. Воспользуемся свойством логарифмов: сумму логарифмов можно представить как логарифм произведения:  . После потенцирования получим уравнение адиабаты:
. После потенцирования получим уравнение адиабаты:
 (4.32)
(4.32)
 Это уравнение показывает, что при адиабатном процессе с изменением объёма давление изменяется на большую величину, чем при изотермическом процессе, поскольку
Это уравнение показывает, что при адиабатном процессе с изменением объёма давление изменяется на большую величину, чем при изотермическом процессе, поскольку  . Рис.4.4, на котором приведены изотерма (пунктирная линия) и адиабата (сплошная линия) для случая, когда начальные параметры состояния газа одинаковы, наглядно показывает это.
. Рис.4.4, на котором приведены изотерма (пунктирная линия) и адиабата (сплошная линия) для случая, когда начальные параметры состояния газа одинаковы, наглядно показывает это.
Используя уравнение состояния идеального газа, можно записать уравнение адиабаты через объём и температуру. Для этого нужно из уравнения состояния идеального газа выразить давление и подставить в уравнение (4.32). После преобразований получим:
 (4.33)
(4.33)
Можно записать уравнение адиабаты через давление и температуру, выразив из уравнения состояния идеального газа, объём через давление и температуру:
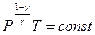 (4.34)
(4.34)
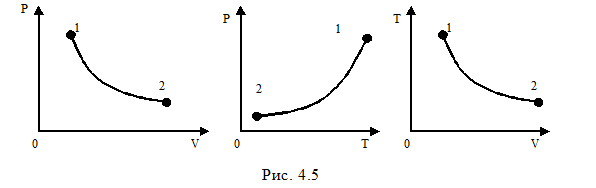 При адиабатном процессе все три параметра состояния изменяются. Это изменение выражено формулами (4.32), (4.33), (4.34). Процесс адиабатного расширения изображён на рис.4.5.
При адиабатном процессе все три параметра состояния изменяются. Это изменение выражено формулами (4.32), (4.33), (4.34). Процесс адиабатного расширения изображён на рис.4.5.
При адиабатном расширении газ совершает работу за счёт убыли собственной внутренней энергии: . Работу адиабатного процесса проще всего рассчитать через изменение внутренней энергии:
. Работу адиабатного процесса проще всего рассчитать через изменение внутренней энергии:  . Поскольку внутренняя энергия идеального газа – функция состояния и зависит только от температуры, то изменение внутренней энергии, а, следовательно, и работу можно найти по формуле:
. Поскольку внутренняя энергия идеального газа – функция состояния и зависит только от температуры, то изменение внутренней энергии, а, следовательно, и работу можно найти по формуле:
 (4.35)
(4.35)
Работу газа при адиабатном процессе можно определить и через элементарную работу: . Для этого будем считать известными начальные параметры состояния P1, V1, T1. Из уравнения адиабаты
. Для этого будем считать известными начальные параметры состояния P1, V1, T1. Из уравнения адиабаты  выразим давление Р:
выразим давление Р:
 . Тогда элементарная работа будет определяться формулой:
. Тогда элементарная работа будет определяться формулой: . При определении работы адиабатного процесса вынесем за знак интеграла известные величины и получим:
. При определении работы адиабатного процесса вынесем за знак интеграла известные величины и получим: 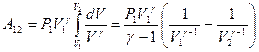 . Вынесем за скобки
. Вынесем за скобки 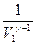 , и после преобразования получим:
, и после преобразования получим:
 (4.36)
(4.36)
Используя уравнение Менделеева – Клапейрона, можно получить другую формулу:
 (4.37)
(4.37)
Из формулы (4.37) можно получить формулу (4.35). Для этого нужно учесть, что 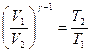 и
и 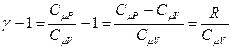 .
.
Следует отметить, что само по себе расширение идеального газа не может привести к его охлаждению, если при расширении газ не производит работу. Это значит, что, если идеальный газ расширяется таким образом, что к сосуду, в котором он находится, присоединяется другой пустой сосуд, то температура газа не изменится. Неизменность температуры обусловлена тем, что внутренняя энергия идеального газа не зависит от объёма. При таком расширении в пустоту идеальный газ не совершает работы.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1565; Нарушение авторских прав?; Мы поможем в написании вашей работы!