VI.- законы коммутативности (переместительности)

V.- законы идемпотентности.

IV.- закон двойного отрицания.

III.- закон исключенного третьего.

II.- закон противоречия.

I.- закон тождества.

ЛЕКЦИЯ

Государственный строй

Форма правления – феодально-теократическое централизованное государство во главе с халифом

к занятию 7 и 8

Тема: Логическая равносильность

План:

1) Равносильность формул логики высказываний.

2) Закон логики.

3) Равносильные преобразования. Упрощение фор­мул.

4) Выражение импликации и эквиваленции через конъюнкцию, дизъюнкцию и отрицание.

1. Равносильность формул логики высказываний. B логике говорят, что предложения равносильны, если они одновременно истинны либо одновременно ложны. Слово «одновременно» в этой фразе неоднозначно. Так, для предложений «Завтра будет вторник» и «Вчера было воскресенье» это слово имеет буквальный смысл: в по­недельник они оба истинны, в остальные дни недели – оба ложны. Для уравнений x=2 и 2х=4 «одновременно» означает «при одних и тех же значениях переменной». Прогнозы «Завтра будет дождь» и «Неверно, что завтра не будет дождя» одновременно подтвердятся (окажутся истинными) либо не подтвердятся (окажутся ложными). В сущности, это один и тот же прогноз, вы­раженный в двух разных формах, которые можно представить формулами Х и 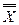. Эти формулы одновременно принимают значение и либо значение л (проверьте!).

Такие формулы, как и соответствующие им предложения, естественно считать равносильными.

Формулы F₁ и F₂ называются равносильными, если их эквиваленция F₁↔F₂ - тавтология.

(Напомним, что эквиваленция истинна тогда и только тогда, когда составляющие ее высказывания оба истин­ны либо оба ложны; следовательно, F₁↔F₂ есть тавто­логия в том и только в том случае, если формулы F₁ и F₂ «одновременно», т.е. при одинаковых наборах значений переменных, входящих в формулы, принимают одинако­вые значения.)

Говорят, что предложения Р₁ и Р₂ равносильны в ло­гике высказываний, если соответствующие им формулы равносильны.

Равносильность двух формул логики высказываний (а также соответствующих этим формулам предложений) будем обозначать символом ≡, запись F₁≡F₂ читается так: «формула F₁ равносильна формуле F₂».

Выражение F₁≡F₂ - не формула в языке логики вы­сказываний. Оно является метаязыковым высказывани­ем о формулах F₁ и F₂, утверждающим, что эти формулы равносильны.

Равносильность есть отношение меж­ду формулами (так же как равенство - это отношение между числами, параллельность — это отношение между прямыми и т.п.).

Легко убедиться, что отношение равносильности об­ладает следующими свойства ми: а) рефлексивности: F≡F;

б) симметричности: если F₁≡F₂, то F₂≡ F₁;

в) транзитивности: если F₁≡F₂ и F₂≡F₃, то F₁≡F₃.

2. Закон логики. Равносильности формул логики высказываний часто называют законами логики. Перечислим наиболее важные из них:

Дата добавления: 2014-01-07