Математические модели процессов в реакторе

Лекция от 14.03.13

Вопрос 5. Понятие прокурорского надзора и его особенности

Вопрос 4. Цели, стоящие перед органами прокуратуры и основные направления деятельности органов прокуратуры

Вопрос 6. Надзор прокуратуры за исполнением законов (общий надзор)

Нормативная основа: статьи 21-25.1 ФЗ «О прокуратуре», а также различные приказы Ген. прокурора РФ. Данное направление надзора является наиболее сложным, так как распространяется на значительный круг поднадзорных субъектов и включает в себя надзор за исполнением практически всех отраслей российского законодательства.

Предмет надзора:

1) Соблюдение Конституции РФ и исполнения законов следующими поднадзорными субъектами: федеральными министерствами, государственными комитетами, службами и иными федеральными органами исполнительной власти.

2) органами законодательной (представительной) и исполнительной власти субъектов РФ.

3) органами местного самоуправления

4) органами военного управления

5) органами контроля

6) должностными лицами всех вышеперечисленных органов

7) органами управления и руководителями коммерческих и некоммерческих организаций

8) субъектами осуществления общественного контроля за обеспечением прав человека в местах принудительного содержания.

2) законность правовых актов, издаваемых всеми вышеперечисленными поднадзорными субъектами. Основания для проведения прокурорской проверки является поступившая в прокуратуру информация о фактах нарушения закона, требующая принятия мер прокурором. Это могут быть направленные в прокуратуру жалобы граждан, материалы проверок контролирующих органов, публикации в средствах массовой информации и иные обращения, для проверки поступившей информации прокуроры наделены определенными полномочиями:

а) по предъявлению служебного удостоверения проверяющий прокурор в праве проходить на территорию и в помещения подконтрольных субъектов, а также требовать для ознакомления любые необходимые документы

Рассмотрим методику построения математического описания (модели) процесса в реакционной зоне реактора.

Общая схема построения имеет следующий вид:

1. Выяснение структуры потоков и представление ее полной схемой, близкой к установленной реальной картине переноса вещества и тепла.

2. Выделение в этой схеме объема, в котором можно принять параметры, характеризующие состояние фазы (температура, концентрация, теплосодержание) постоянными (назовем его элементарным объемом). Часто можно принять и скорость химического превращения постоянной в этом объеме.

3. Определение процессов в этом объеме и входящих и выходящих потоков. Считаем, что закономерности этих составляющих процессов известны, либо их надо определить расчетным или экспериментальным путем.

4. Составление уравнений материального и теплового балансов, имеющих структуру:

, (1)

, (2)

где Ni, q – количество i- го вещества и тепла в элементарном объеме; SNi внеш, Sqi внеш – потоки i -го вещества и тепла, входящие в элементарный объем и выходящие из него (внешние потоки); SNi ист, Sqi ист – скорости образования i -го вещества и выделения тепла источники внутри объема.

Входящие и выходящие потоки включают:

- потоки гидродинамические (конвективные) SNi конв. Sqi конв.;

- потоки за счет явлений диффузионного типа SNi диф. и Sqi диф.;

- потоки за счет межфазного контакта и теплопередачи к стенке (обмен с другой фазой) SNi фаз, Sqi фаз.

SNi внеш = SNi конв + SNi диф + SNi фаз (3)

Sqi внеш = Sqi конв + Sqi диф + SNi фаз (4)

При этом принимают, что входящие в объем потоки положительны, выходящие – отрицательны. Внутренние источники тепла и вещества – это изменение тепла и вещества, в основном за счет химических реакций. Учитывая, что скорости реакций и превращений относятся к единицы реакционного объема, можно записать

SNi ист = Wi (c,T) dV_p (5)

Sqi ист = SQ_pj r_j(c,T) dV_p (6)

где Wi – скорость химической реакции по i компоненту; Q_pj – тепловой эффект j –той стадии химической реакции; j – номер стадии реакции (в случае сложной схемы реакции); r_j – скорость j –той стадии химической реакции; dVp – элементарный объем.

Левые части уравнений (1) и (2) описывают искомые вещества и количество тепла в элементарном объеме.

Уравнения материального и теплового балансов записывается для каждого вещества. Кроме того уравнения (1) и (2) записываются для каждой фазы.

К уравнениям (1) и (2) необходимо добавить начальные и граничные условия.

Эти уравнения с начальными и граничными условиями представляют собой математическое описание, или модель процесса. Структура уравнений отражает все происходящие явления. Значения коэффициентов, как правило, при этом определены, если установлены составляющие процесса и получены их количественные закономерности.

Построим математические модели для процессов с различными режимами движения потоков. Будем рассматривать реакции, протекающие без изменения объема реакционной смеси и с постоянными теплофизическими свойствами и параметрами тепло и массопереноса, что позволит представить методику построения моделей без усложнения выкладок.

Реактор с полным перемешиванием реагентов без потока вещества через него

(непроточный РИС-п)

«Реактор» (или режим) идеального смешения периодический (PИC – п). В реакционной зоне этого реактора С и Т (концентрация и температура) одинаковы по всему объему, т.е. элементарным объемом будет объем всего реактора dV_p= V_p. Отсутствие потока через реактор означает, что

S Ni_внеш = 0.

Тогда

. (7)

Количество вещества N_i = V_pC_i, так что ,

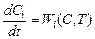. (8)

Для расходуемых веществ Wi (C,T) < 0 и концентрация со временем уменьшается для продуктов со скоростью реакции Wi(C,T) > 0 C_i для них растет.

Для уравнения теплового баланса Sqi внеш определяется только потоками тепла к нагревателю или холодильнику через стенку теплообменника, т.е.

, (9)

где K_T – коэффициент теплопередачи; F_T – площадь поверхности теплообмена; T_x – температура хладагента или нагревателя.

Количество тепла в реакторе определим:

q = V_p C_p T, (10)

где C_p – теплоемкость реакционной смеси,

тогда

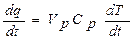. (11)

Используя соотношения (9) – (11) из (2) получим:

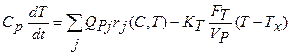. (12)

Начальные условия заданы концентрацией реагентов и температурой в начальный момент процесса, т.е.

при t = 0 T = T_0. (13)

Для дифференциальных уравнений первого порядка (8) и (12) для полного описания задачи требуется два дополнительных условия (13).

Таким образом, система уравнений (8), (12), (13) становится замкнутой, т.е. является систематическим описанием процесса в РИС – п.

Реактор идеального смешения проточный (непрерывный) (РИС –н)

Если через реактор с полным перемешиванием реагентов есть поток реагентов (система открытая), то возможно установления стационарного состояния, не зависящего от времени, как и в предыдущем случае dV_p = V_p. В реактор входят вещества v₀ ×C_{i 0} и выходят v₀ ×C_i (v₀ - расход вещества). Других потоков через реактор нет, так что

. (14)

Тогда (1) примет вид

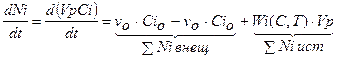(15)

или

, (16)

где - среднее время пребывания в реакционной смеси в зоне реакции.

Отметим, что t определено только через отношение объема к скорости потока и не соответствует физическому времени пребывания реакционной смеси в реакторе. например скорость потока (объемная), как правило определяется при нормальных (или стандартных) условиях, отличных от текущих условий в реакторе.

В реактор входит количество тепла с потоком v₀ C_PT₀, выходит с потоком v₀ C_PT (это конвективная составляющая) и отводится тепло через теплообменную поверхность

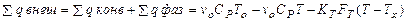(17)

V_P C_P v₀C_pT₀-v₀C_PT - K_TF_T(T-T_x) + ∑Q_Pj r_j (С,T). ∑q _конв ∑q _фаз ∑q _ист dq/dt (18) ∑q _внеш

Тогда

Используя принятые выше обозначения,

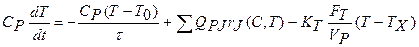. (19)

Если отвода тепла нет, то последнее слагаемое в уравнении в уравнении (19) отсутствует.

Начальные условия заданы концентрацией реагентов и температурой в момент начала процесса (входная величина C_0j, T₀)

t=0 C_j = C_0j; T =T₀ (20)

Система уравнений (16), (19), (20) замкнута и представляет математическое описание процесса в РИС-н

В случае стационарного режима, т.е. когда

система уравнений (16), (19) преобразуется в систему алгебраических уравнений. Для ее решения не требуется дополнительных условий.

Модели идеального смещения соответствуют процессам, происходящим в цилиндрических аппаратах со сферическим дном в условиях интенсивного перемешивания при наличии отражательных перегородок.

Модель идеального вытеснения (РИВ).

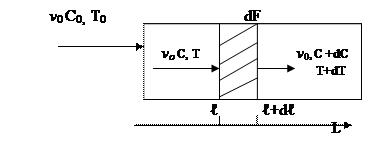
Зона потока соответствует модели идеального вытеснения, если в поперечном сечении происходит идеальное перемешивание, а в продольном (осевом) направлении перемешивание полностью отсутствует. На практике этому условию в первом приближении удовлетворяют трубчатые аппараты. Основным свойством зоны идеального вытеснения, является то, что состояние вещества потока зависит в ней от пространственной координаты – расстояния от входа в зону, поэтому модель зоны идеального вытеснения относится к моделям с распределенными параметрами.

Если в реакторе отсутствует полное перемешивание потока, то концентрация и температура меняются по его объему. Поэтому за элементарный объем будет часть реакционной зоны толщиной dℓ и сечением S. Его объем δV_P = Sdℓ. В этот объем входит вещество v ₀ × C и выходит v ₀ × (C+dC). Других потоков нет, так что

∑N_{i внеш} = ∑Ni _конв = v ₀ × C – v ₀ × (C-dC) = - v ₀ × dC. (21)

Уравнение (1) примет вид:

_. (22)

Поскольку N_i = C_i dV_P = C_i S∙dℓ, (23)

то после подстановки (23) в (22) несложно получить

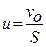
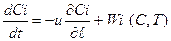, (24)

где - линейная скорость потока.

Тепловой поток через элементарный объем состоит из конвективной составляющей

åq _конв =v₀ C_P T – v₀ C_P (T + dT) = -v₀ C_P dT (25)

потока тепла, через стенку поверхностью dF_T (поскольку и обмен дифференциально малый)

åq _фаз = K_T dF_T (T-T_X)

Уравнение (2) примет вид:

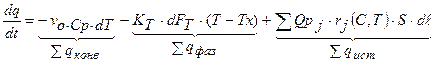. (26)

Поскольку q = dV_P × C_PT = S × dℓ C_PT, следовательно:

Определим удельную поверхность теплообмена

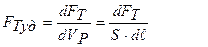. (27)

Тогда уравнение (25) преобразуется к следующему виду:

Чтобы решить систему двух дифференциальных уравнений (24), (27), т.е. замкнуть систему дифференциальных уравнений нужны два дополнительных условия. Ими будут условия на входе в реактор при

r = 0 (ℓ = 0) Ci = Ci₀ T = T₀ (28)

Система уравнений (24), (27), (28) – систематическое описание (модель) процесса РИВ

Дата добавления: 2014-01-07