Связь между моделями Мили и Мура

Рассмотрим некоторый автомат Мили, заданный таблицами переходов и выходов. Таблица переходов а) и выходов б) автомата Мили

Подадим на вход автомата, установленного в состояние а₁, входное слово x=z₁ z₂ z₂ z₁ z₂ z₂. Так как d(а₁, z₁) = a₂, l(a₁, z₁) = W₂, то под воздействием входного сигнала z₁ автомат перейдет в состояние а₂ и выдаст на переходе выходной сигнал W₂. Затем, находясь в состоянии а₂ под воздействием сигнала Z₂ перейдет в состояние а₁=d(а₂, z₂) и выдаст сигнал W₁=l(a₂, z₂) и т.д. В табл. 13 приведена последовательность состояний, которые автомат проходит, воспринимая входное слово x, и выходные сигналы, вырабатываемые на этих переходах.

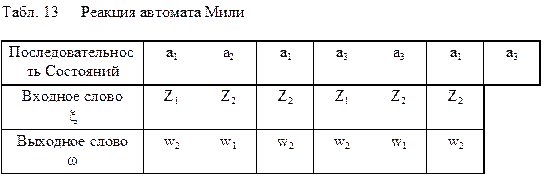
Назовем выходное слово w = l (a_1, x) реакцией автомата Мили в состоянии а₁ на входное слово x.

В нашем случае w = w₂ w₁ w₂ w₂ w₁ w₂

Как видно, из приведенного примера, в ответ на входное слово длины k автомат Мили выдаст последовательность состояний длины k +1 и выходное слово длины k.

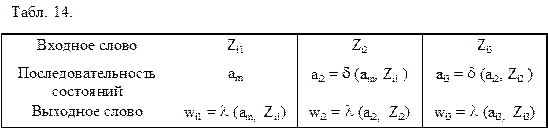
В общем виде поведение автомата Мили, установленного в состояние a_m, можно описать следующим образом (табл. 14).

Аналогично можно описать поведение автомата Мура, находящегося в состоянии a₁, при приходе входного слова

x = Z_i1, Z_i2,..., Z_ik,учитывая, что W(t) = l(a(t)):

Входное слово	Zi1	Zi2	Zi3	Z
Последовательность cостояний	am	ai2 = d (am, Zi1)	ai3 = d (ai2, Zi2)	ai4 = d(ai3, Zi3)
Выходное слово	wi1 = l (am, Zi1)	wi2 = l (ai2, Zi2)	wi3 = l (ai3, Zi3)	wi4 = l (ai4)

Очевидно, что для автомата Мура выходной сигнал W_i1= l(a_m) в момент времени i₁ не зависит от входного сигнала Z_i1 и определяется только состоянием a_m. Следовательно, сигнал W_i1 никак не связан с входным словом x.

В связи с этим под реакцией автомата Мура, установленного в состояние a_m, на входное слово x = Z_i1, Z_i2,..., Z_ik будем понимать выходное слово той же длины w = l(a_m, x) = W_i2 W_i3...W_ik+1, сдвинутое по отношению к x на один такт.

Рассмотрим пример. Пусть задан автомат Мура:

Подадим на вход этого автомата ту же последовательность, что и для автомата Мили: x=z₁ z₂ z₂ z₁ z₂ z₂. Последовательность смены состояний и вырабатываемых выходных сигналов представлена в таблице:

	w1	w2	w3	w4
	a1	a2	a3	a4
z1	a2	a3	a4	a4
z1	a4	a1	a1	a1

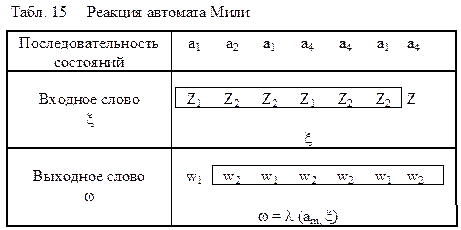
Сравнивая реакции автомата Мили (табл. 13) и автомата Мура (табл.15), отмечаем, что эти реакции на одно и то же слово x совпадают. Следовательно автоматы Мили и Мура реализуют одно и то же преобразование слов входного алфавита. Такие автоматы называются эквивалентными. Строгое определение эквивалентности следующее:

Дата добавления: 2014-01-07