Метод парабол

Пусть f (x) имеет первую и вторую производную. Разложим f (x) в ряд Тейлора в некоторой точке x _k, ограничиваясь при этом тремя членами разложения:

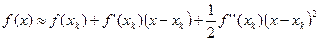. (3)

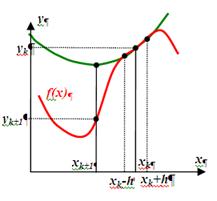Иными словами, аппроксимируем нашу функцию в точке x _k параболой. Для этой параболы можно аналитически вычислить положение экстремума как корень уравнения первой производной от (3): . Пусть минимум аппроксимирующей параболы находится в точке x _k+1. Тогда вычислив значение функции f (x _k+1), мы получаем новую точку приближения к минимуму.

Обычно в практических реализациях данного метода не используют аналитический вид первой и второй производных f (x). Их заменяют конечно-разностными аппроксимациями. Наиболее часто берут симметричные разности с постоянным шагом h:

;

.

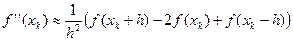Это эквивалентно аппроксимации функции параболой, проходящей через три близкие точки x _k+ h, x _k, x _k– h. Окончательное выражение, по которому можно строить итерационный процесс, таково:

. (4)

Данный метод отличается от вышеизложенных высокой скоростью сходимости. Вблизи экстремума, вплоть до расстояний ~ h ², сходимость практически не отличается от квадратичной. Однако алгоритм требует постоянного контроля сходимости. Например, итерационный процесс будет сходиться к минимуму, если

1) знаменатель формулы (4) должен быть >0. Если это не так, нужно сделать шаг в обратном направлении, причем достаточно большой. Обычно в итерационном процессе полагают 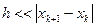. Иногда ради упрощения расчетов полагают 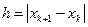, однако это существенно уменьшает скорость сходимости.

2) 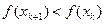. Если это не так, то от x _k следует сделать шаг 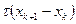с τ = ½. Если и при этом условие убывания не выполнено, уменьшают τ и вновь делают шаг.

Дата добавления: 2014-01-07