С помощью функции rkfixed

Решение обыкновенных дифференциальных уравнений

Встроенная функция rkfixed (метод Рунге – Кутта с фиксированным шагом решения) позволяет решать только обыкновенные дифференциальные уравнения (ОДУ) первого порядка или системы таких уравнений. Уравнения порядка выше первого требуется преобразовывать в систему уравнений первого порядка.

Задача Коши для ОДУ n–го порядка ставится следующим образом: найти решение уравнения при заданных начальных условиях:

y⁽ⁿ⁾=f(x,y,y',y'',…,y^(n-1))

y(x₀)=y₀

y'(x₀)=y₀₁ (7)

……………….

y^(n-1)(x₀)=y_0(n-1),

здесь y^(m) - производная m порядка от решения, m=1,2,…,n.

Основной прием, используемый при решении задач типа (7), заключается во введении новых переменных и сведении задачи решения ОДУ высокого порядка к решению системы уравнений первого порядка. Введем новые переменные

y₁=y

y₂=y'

…………

y_n=y^(n-1),

тогда задачу (7) можно представить в виде системы n ОДУ первого порядка:

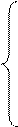y'₁=y₂

………………

y'_n-1=y_n

y'_n=f(x,y₁,…,y_n-1) (8)

y₁(x₀)=y₀₁

y₂(x₀)=y₀₂

……………….

y_n(x₀)=y_0n.

Пусть необходимо решить задачу Коши для ОДУ второго порядка:

y''=f(x,y,y')

при заданных начальных условиях:

y(x₀)=y₀ (9)

y'(x₀)=y₀₁.

Путем введения замены y₁=y сведем (9) к системе

y'₁=y₂

y'₂= f(x, y₁,y₂) (10)

y₁(x₀)=y₀₁

y₂(x₀)=y₀₂.

Пример. Решим методом Рунге-Кутта с фиксированным шагом дифференциальное уравнение второго порядка, описывающее колебательное звено:

T² y'' + 2ξT y' + y = 0 или y'' = - 2ξ/T y' - 1/T² y

при заданных начальных условиях t₀ =0, y(t₀)=1, y'(t₀)=0 и заданном конце счета t_k= 13. Здесь Т- постоянная времени, ξ – коэффициент затухания.

Система уравнений (10) примет следующий вид:

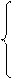y'₁=y₂

y'₂= - 2ξ/T y₂ - 1/T² y₁ (11)

y₁(t₀)=1

y₂(t₀)=0.

Записав правые части и начальные условия в виде векторов, получим

y₂ 1

F(t,y)=, v=,

- 2ξ/T y₂ - 1/T² y₁ 0

где F(t, y) – это вектор правых частей системы, v – вектор начальных условий.

При формировании данного вектора надо обратить внимание на следующее:

1. Вместо буквы F можно использовать любую другую букву. Но тогда и в параметрах встроенной функции нужно, естественно, использовать ту же букву.

2. Внутри скобок первое имя (в данном примере t) является именем аргумента, по которому происходит интегрирование дифференциального уравнения. Ранее в тексте использовалась буква x.

3. Вторая буква внутри скобок – это вектор имен зависимых переменных. Если принято имя y, то именами переменных должны являться y₁, y₂ и т.д., причем первое уравнение – это

dy₁ /dt =……, второе

dy₂/dt = …… и т.д.

Выполним численное решение (11) для следующих значений параметров колебательного звена: Т=2, x =0.3. Для этого необходимо загрузить программу SMath Studio и ввести в программу параметры дифференциальных уравнений (T, ξ), начальные условия, векторы правых частей системы уравнений и оформить встроенную функцию rkfixed, как показано на рис. 3. Здесь необходимо обратить внимание на разное написание нижних индексов у элементов массива y₁, y₂ (управление символом «[») и подстрочных символов t₀ и t_k (управление символом ”.”).

После щелчка левой кнопкой мыши по свободному месту рабочего поля выполняется решение задачи. Фрагмент матрицы Y численного решения уравнения показан на рис. 3.

Рис. 3

В первом столбце показаны значения аргумента (время), во втором – сама функция и в третьем – производная. Для вывода матрицы на экран необходимо выполнить ее умножение на единицу и ввести оператор присвоения.

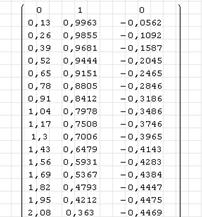
Рис. 3

Для построения графиков полученного решения необходимо с помощью функции col (Имя массива; Номер столбца массива) сформировать из столбцов матрицы Y вектора, которые используются функцией augment для построения графиков (рис. 4).

Рис. 4

По оси абсцисс графика (рис. 5) отложен первый столбец матрицы, по оси ординат отложены переменная y(t) (кривая 1) и ее производная (кривая 2).

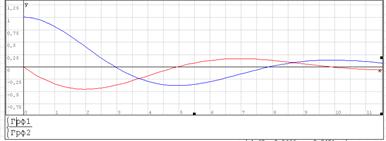
Рис. 5

Дата добавления: 2014-01-07