Решение системы уравнений методом прогонки

Метод прогонки, так же как и метод Гаусса, разделяется на два этапа: прямой и обратный ход. В результате прямого хода вычисляются вспомогательные переменные, называемые прогоночными коэффициентами. На обратном ходе получают значения неизвестных.

Метод прогонки специально создан для решения систем линейных алгебраических уравнений с трехдиагональной матрицей, т.е. для систем вида (5).

Рис. 1

Системы такого вида часто возникают при решении различных задач вычислительной математики (например, при численном решении дифференциальных уравнений и интерполировании сплайнами)

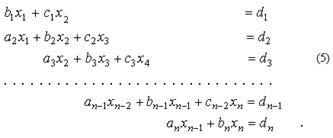
Для решения системы уравнений выразим x₁ из первого уравнения системы (5):

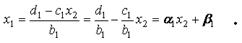(6)

Выражение для x₁ подставим во второе уравнение системы (5):

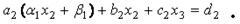
Выражая из последнего соотношения x₂, получаем:

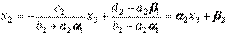. (7)

Выражение для x₂ подставим в третье уравнение системы (5) и так далее. На i-м шаге описанного процесса (1 < i < n) i-е уравнение системы приводится к такому же виду:

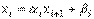, где

(8)

,

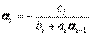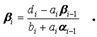
На последнем n-м шаге подстановки получаем n-е уравнение в виде 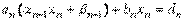. Отсюда можно выразить неизвестное x_n:

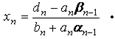(9)

Значения остальных неизвестных вычисляются в процессе обратного хода по формулам (8).

Таким образом, прямой ход состоит в вычислении прогоночных коэффициентов 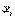и 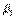по формулам:

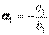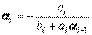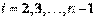, , , (10)

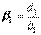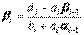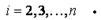, , (11)

Обратный ход метода прогонки дает значения неизвестных по формулам:

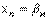
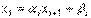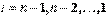, . (12)

Отметим, что метод прогонки относится к классу экономичных методов. Экономичными называются методы, для которых число требуемых арифметических операций пропорционально числу неизвестных. Для реализации вычислений по описанному алгоритму требуется примерно 8n арифметических операций (тогда как в методе исключения Гаусса эта величина примерно 2 n³/3). Экономичность в данном случае достигается за счет того, что при реализации метода не выполнялись операции над нулевыми элементами исходной матрицы.

Пример использования метода прогонки (алгоритма Томаса) для решения у трёхдиагональной системы линейных уравнений представлен на рис. 2. Пользователь задаёт матрицу коэффициентов уравнений и столбец ответов. Результат сравнивается с ответом встроенного средства решения линейных уравнений программы (метод обратной матрицы).

Трехдиагональной матрицей называют матрицу вида .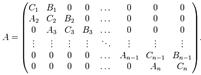

Задание. При выполнении лабораторной работы необходимо изучить программную реализацию метода прогонки (рис. 2), ввести программу в компьютер и решить примеры в соответствии со своим вариантом.

Дата добавления: 2014-01-07