Закон Архимеда

Архимед (287 – 212 г. до н.э.) рассмотрел задачу о телах, погруженных в жидкость. Он установил, что вес тела, погруженного в жидкость, уменьшается, что связано с действием на тело выталкивающей силы или силы Архимеда. Эта сила возникает из-за того, что давление жидкости увеличивается с глубиной, поэтому сила, действующая на тело сверху вниз, меньше силы давления, направленной снизу вверх.

Закон Архимеда. На тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (газа) выталкивающая сила, численно равная весу вытесненной телом жидкости (газа), в объеме погруженной части тела, линия действия которой направлена в сторону, противоположную весу вытесненной жидкости и проходит через центр тяжести вытесненной жидкости (газа).

Доказательство закона Архимеда.

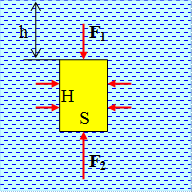
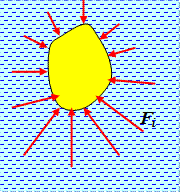
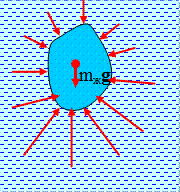
Рис. 5.2.1. Рис. 5.2.2. Рис. 5.2.3.

1. Рассмотрим, для простоты, тело в форме прямоугольного параллепипеда или цилиндра, погруженного в жидкость плотности r (рис. 5.2.1). Найдем результирующую поверхностных сил давления, действующих на тело. Силы, действующие на боковую поверхность тела, стремятся сжать его, они взаимно уравновешены. Тогда выталкивающая сила равна ,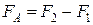

где 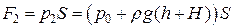и 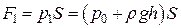. Откуда получим

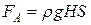, Þ 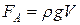. (5.2.1)

Замечание. Если тело погружено в жидкость не полностью, а частично, под объемом V в формуле (5.2.1), следует понимать объем погруженной части тела.

2. Докажем закон Архимеда в общем случае тела произвольной формы (рис. 5.2.2). Для этого используем принцип отвердевания.

На тело, погруженное в жидкость (рис. 5.2.2), действуют поверхностные силы давления, результирующая которых равна выталкивающей силе:

.

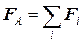Мысленно удалим тело и заполним образовавшуюся полость жидкостью (рис. 5.2.3). Очевидно, что при этом равновесие жидкости в сосуде не нарушается. Жидкость, которая заняла место удаленного тела, можно считать отвердевшей. На эту жидкость действует сила тяжести 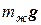, приложенная к ее центру тяжести. Кроме того, на нее действуют со стороны окружающей жидкости те же поверхностные силы давления 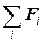, которые действовали на тело. Как и вся жидкость, этот отвердевший объем находится в равновесии, т.е.

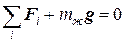.Þ .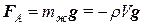

Для того, чтобы была равна нулю и сумма моментов внешних сил относительно оси, проходящей через центр тяжести отвердевшего объема, результирующая сил давления должна проходить через центр тяжести.

Тем самым доказаны все утверждения закона Архимеда.

Сила Архимеда в неинерциальной системе отсчета.

1. Ускорение a системы направлено вертикально вниз.

Т.к. гидростатическое давление в этом случае вычисляется по формуле (5.1.4): 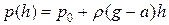, то сила Архимеда равна

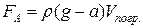(5.2.2)

В невесомости сила Архимеда отсутствует: F_A = 0.

Если ускорение a системы направлено вертикально вверх, то

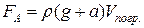(5.2.3)

2. Ускорение a системы направлено горизонтально. (рис. 5.2.4)

Уровень жидкости в этом случае наклонен под углом a: .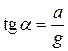

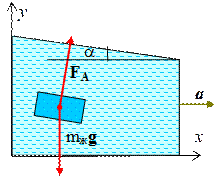
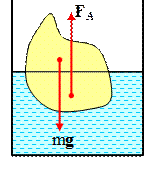
Рис. 5.2.4. Рис. 5.2.5.

Получим формулу для силы Архимеда. Мысленно удалим тело и заполним образовавшуюся полость жидкостью. Эта жидкость, массой m_ж, будет двигаться с ускорением a. Тогда

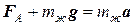. Þ 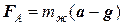. (5.2.4)

Направление выталкивающей силы совпадает с вектором a – g, т.е. сила Архимеда перпендикулярна поверхности жидкости. Формула (5.2.4) позволяет найти силу Архимеда в случае произвольного направления вектора a. Если вектор a – горизонтален, то

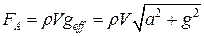. (5.2.5)

Условия плавания. (рис. 5.2.5)

1. Тело тонет, если 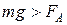, т.е. средняя плотность тела больше плотности жидкости: .

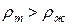2. Тело всплывает, если 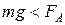, т.е. средняя плотность тела меньше плотности жидкости: 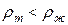. Положение равновесия плавающего тела - устойчивое равновесие. При этом выталкивающая сила равна

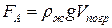, (5.2.6)

где V_{погр .} – объем погруженной части тела.

Устойчивость плавания корабля.

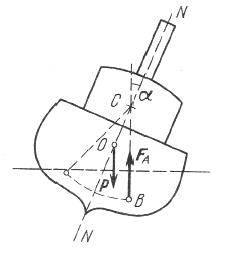
Рис. 5.2.6.

Для строительства кораблей большое значение имеет вопрос устойчивости его плавания. На рис. 5.2.6 изображен корабль, накрененный на некоторый угол a от вертикального положения. При этом центр тяжести вытесненной кораблем воды в наклоненном положении (точка приложения выталкивающей силы) находится в точке B, смещенной из плоскости симметрии корабля NN в ту же сторону, куда накренился корабль. Проведем через точку B вертикаль, которая представляет собой линию действия выталкивающей силы. Точка C пересечения линии действия выталкивающей силы наклоненного корабля с плоскостью симметрии корабля называется метацентром.

Если метацентр лежит выше центра тяжести корабля O, то момент выталкивающей силы относительно центра тяжести корабля стремится возвратить корабль в вертикальное положение, т.е. корабль плавает устойчиво.

Если же метацентр лежит ниже центра тяжести корабля O, то плавание корабля в вертикальном положении будет неустойчивым.

Дата добавления: 2014-01-07