Индексация граней

Широта области гомогенности

Критерии чистоты вещества определяется его физическими свойствами: температурами кипения, плавления, плотностью, строением кристалла. Закон постоянства состава выполняется для газов и жидкостей. Кристаллические вещества сохраняют свою структуру при переменном (в некоторых пределах) составе. Пределы колебаний состава при сохранении кристаллической структуры называется широтой области гомогенности.

Обычно ионные кристаллы имеют небольшую широту области гомогенности (1-5%), однако для таких кристаллов уже нельзя полностью применять закон постоянства состава. Значительно больше широта области гомогенности у соединений металлов с углеродом, бором, Si, N, H и Cl, сохраняющих до известной степени металлический, характер связи (электропроводность).

Для описания положения граней кристалла естественно пользоваться приёмами аналитической геометрии, а именно системой осей координат. Но если в аналитической геометрии предпочитают декартовы координаты (угол между осями составляет 90°), то в кристаллографии выбирают систему координат так, чтобы оси координат были параллельны рёбрам кристалла.

Положение любой грани кристалла можно задать так называемыми параметрами грани x, y, z. Параметрами грани называются величины отрезков, отсекаемых плоскостью грани на осях, причём за единицу приняты величины отрезков, отсекаемых единичной гранью. (рис 11.)

рис.11. Параметры грани

Казалось бы, простой метод описания положения граней совокупностью параметров x, y, z вполне удовлетворителен. Но в кристаллографии и рентгенографии пользуются не параметрами, а индексами грани h, k,ℓ. Индексы грани позволяют выбрать грань с нужными свойствами. Учёт индексации приводит к возможности выращивать монокристаллы с определёнными свойствами. Индексы грани – это величины, обратно пропорциональные параметрам грани x, y, z. Следовательно, если плоскость отсекает на осях отрезки x, y, z, то вместо отношения отрезков x: y: z берут отношение:

1/x: 1/y: 1/z = h: k: ℓ

Совокупность индексов грани называется символом грани. Символ грани в общем случае записывается (h k ℓ); символ единичной грани (III). Параметры h, k, ℓ называются индексами Миллера.

Если плоскость пересекает ось в области отрицательных значений координат, то соответствующий индекс будет отрицательным и знак минус ставится над индексом.

Непараллельные плоскости, имеющие одинаковое атомное строение, кристаллографически эквивалентны (например, (001), (100) или (110) и (011) и т.д.).

Зная индексы (hkl) плоскости, можно подсчитать межплоскостное расстояние d между плоскостями (hkl) данного семейства для кубических кристаллов с периодом решетки a по формуле

Эта зависимость широко используется при рентгеноструктурном анализе кристаллических тел, имеющих кубическую решетку.

Индексы Миллера. Служат для характеристики положения произвольной кристаллической плоскости в кристаллографической системе осей (рис. 11).

1. Если плоскость параллельна оси, то точка пересечения плоскости с осью находится в бесконечности. Обратное значение:

1/∞=0.

2. Символ {hkl}. Обозначает семейство всех равнозначных кристаллографических плоскостей.

Например: {100} — простая кубическая решетка; может быть получена следующей комбинацией (hkl):

{hkl}	Плоскость
hkl = (100) hkl = - (100) hkl = (010) hkl = - (010) hkl = (001) hkl = - (001)	Передняя Задняя Правая Левая Верхняя Нижняя

3. Символ [uvw] — направление в решетке. Это направление, которое проходит от начала координат к произвольной точке Р кристаллической решетки; оно может однозначно характеризоваться координатами и, v, w точки Р, которые и обозначаются символами [и, v, w].

4. Символ <uvw>. Применяется в тех случаях, когда нужно характеризовать только симметрию, а не положения решетки в пространстве.

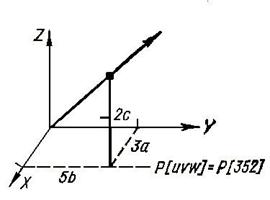
При обо­­­зна­чении узлов и направ­ле­­ний в кристал­ли­чес­кой ре­ше­­т­ке ко­ор­ди­­на­ты лю­­бого уз­ла ре­­шетки можно вы­ра­зить как x=m × a, y=n × b, z=p × c, где a, b, c - параметры ре­шетки, m, n, p - це­лые или дро­бные числа. Если за еди­ницы измерения длин при­нять параметры ре­ше­тки, то ко­ор­­ди­на­та­ми узла бу­дут просто це­лые или дро­бные числа m, n, p. Эти числа на­зы­вают индексами уз­ла и за­пи­сывают сле­ду­ю­щим об­разом: [[ mnp ]] (рис. 12, а).

Рис. 12.

Рис. 13.

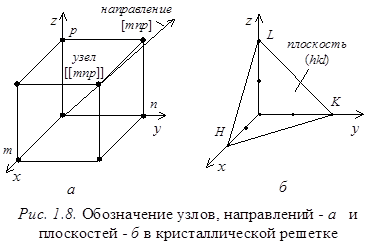
Для удобства опи­сания гексагональной решетки часто к трех­ос­ной сис­те­ме координат до­ба­вляют четвертую координатную ось u, ко­­то­рая составляет ра­в­ные углы (120^o) с осями x и y и пер­пе­н­ди­ку­ля­­р­на гексагональной оси z (рис. 13, г). В получившейся че­тырех­о­с­ной системе ко­ор­ди­нат (x, y, u, z) каждая из граней элементарной гексагональной ячей­ки пе­­ресекает по две ко­ор­­ди­нат­ные оси, от­се­кая от них оди­­на­ковые от­ре­­зки. Про­е­к­ции узловых точек на оси ко­ор­динат x, y, u, z могут пре­д­­с­та­­влять собой дробные или от­ри­ца­те­ль­ные числа.

По­с­ле при­ве­­дения к об­щему знаменателю числители по­­лу­чен­ных дробей яв­ля­ю­­тся ин­де­­ксами направления. В ка­че­стве при­­мера на рис. 13, г при­ве­­­дены ин­дексы координатных осей x, y, u. Зна­­че­ния индекса, ме­нь­ше нуля, отмечены знаком инверсии над со­­от­­­ве­т­ствующим ин­де­к­сом. Например, ко­ор­ди­на­ты узла B, ле­жащего на оси y (рис. 13, г) ра­­в­ны [[-1/2, 1, -1/2, 0]]. Сле­до­ва­те­ль­­но, индексы на­­правления, со­в­па­да­ющего с осью y, равны 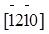. Индексы направлений ко­ор­ди­натных осей х и u ра­в­ны 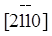и 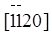соответственно.

Пример 1. Определить индексы плоскости, параллельной осям у и z/

Решение: Если лучи падают

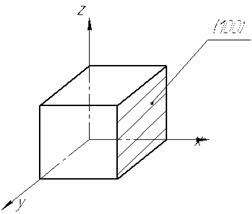X=a перпендикулярно плоскости 100,

Y=∞ то они встретят две плоскости и Z=∞ расстояние между ними равно h:k:l=1:0:0 d₁₀₀=a

x: y:z =a: ∞:∞

h:k:l =(1/a):(1/∞):(1/∞)=1/a:0:0=1:0:0;

Следовательно, символ грани (100).

Пример 2. Определить индексы грани в простой кубической решетке, параллельной оси z.

Решение: Если лучи перпендикулярны

X=a плоскости 110, то d=a2¹/₂ 2, так Y=a как плоскостей будет уже 3 и Z=∞ расстояние равно половине диагонали куба.

x: y: z=a: a: ∞

h: k: l = (1/a): (1/a): (1/∞) =(1/a): (1/a): 0

Символ грани (110)

Пример 3. Определить индексы Миллера в простой кубической решетке в случае x=a, y=a, z=a.

Решение:

h: k: l = 1/a: 1/a: 1/∞ =1: 1: 1

Если лучи падают перпендикулярно грани 111, то они уже встретят 4 плоскости и расстояние между ними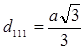

Символ грани (111).

Пример 4. Определить расстояние между плоскостями (100).

Решение:

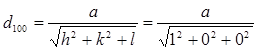
Отношение обратных величин d₁₀₀, d₁₁₀, d₁₁₁, является характеристикой для данного типа кристаллической решетки: 1/d₁₀₀: 1/d₁₁₀: d₁₁₁=1:2^½:3^½. Это соотношение построения для данной решетке, в конечном итоге определяет отношения расстояние на рентгенограмме кристалла.

Дата добавления: 2014-01-07