Тема: дифракція

ПЛАН

1. Принцип Гюйгенса-Френеля. Метод зон Френеля.

2. Дифракція на круглому отворі, дискові.

3. Дифракція на одній щілині. Дифракційна решітка.

4. Дифракція на просторовій решітці.

1. Дифракція - це явище відхилення світла від прямого поширення, яке виникає у середовищи із різко вираженими неоднорідностями (а ~ l; l ³ а, де а - розмір перешкоди).

Основні положення принципу Гюйгенса:

а) кожна точка хвильового фронту хвилі є джерелом нових сферичних хвиль;

б) результуюча хвиля у будь-який час являє собою результат інтерференції всіх вторинних хвиль.

Цей принцип однак не дає методу знаходження результуючої амплітуди у будь-якій точці простору. Це дає метод зон Френеля.

Метод зон Френеля:

Маємо джерело світла S. На відстані R від нього поширюється сферична хвиля з вершиною в точці В. Відстань від екрана (спостерігач) до точки В - r₀.

B₃ r₃

R B₂ r₂

S * B₁ r₁ D

B

r₀

На сферічній поверхні вибираємо систему точок В₁, В₂ і т.д. таким чином, щоб відстань від спостерігача (Д) до кожної наступної точки була більша на l/2.

r₁ = r₀ + l/2

r₂ = r₁ + l/2 = r₀ + 2l/2

r₃ = r₀ + 3l/2

....

r_k = r₀ + kl/2

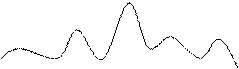
Завдяки такому вибору точок В_і на сферичній поверхні будемо мати зони Френеля одинакової площі S₁ = S₂ = S₃ =...

I

II

III

Коливання, які спостерігаються в точці Д двома будь-якими сусідніми зонами, протилежні за фазою (D £ l/2), амплітуди цих коливань, мають протилежні знаки. Якщо а₁, а₂ - амплітуди коливань, збуджувані 1, 2... зонами Френеля, то результуюча амплітуда у точці Д має такий вигляд:

a₁ - a₂ + a₃ +… - a_2k + a_2k+1

А = а₁ - а₂ + а₃... + а_2к+1 - а_2к

Можна показати, що для близько розташованих зон залежність к від А буде лінійною і тому:

,

тоді члени, які стоять в дужках, дорівнюють нулю:

А= a₁/2

А звідси висновок: якщо маємо відкритий фронт хвилі, то результуюча дія у точці Д складових хвиль дорівнює половині амплітуди першої зони Френеля.

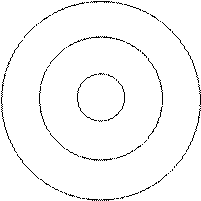
2. Маємо диск радіусом R, на який падає світ. Розглянемо дію сферичних хвиль на круглому дискові.

B

r₀ r₀ + 2l/2 F

Застосувавши метод Френеля можна одержати, що результуюча амплітуда у точці В буде дорівнювати непарній кількості зон Френеля:

.

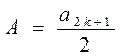Тому в точці В будемо мати світле пятно. А якщо взяти замість диска круглий отвір, то в результаті будемо мати к відкритих зон Френеля. Світло чи темрява буде в точці В залежатиме від того, парною чи непарною буде кількість зон Френеля.

Якщо к парне – буде темрява, а якщо к непарне – буде світло.

3. Розглянемо дифракцію паралельного пучка променів, які падають на щілину шириною а.

a

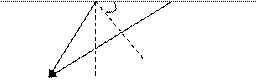j

j D

B Eкран

D = а sin j

min: a sin j = ± 2k l/2

max: a sin j = ± (2k + 1)l/2

k – кількість зон Френеля.

Якщо парна кількість зон Френеля – темрява, а якщо непарна – світло.

к = 1, 2, 3... – порядок дифракційного максимуму або мінімуму.

j_к – кут дифрації. Це кут, під яким спостерігається к-ий дифракційний максимум.

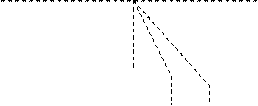
Розглянемо дифракційну ґратку – систему щілин, розділених непрозорими проміжками:

b

a

j₁

j₂

Eкран

d = a + b (період – стала дифракційної решітки).

Умови головних max i min:

max: d sinj = ± 2k (l/2)

k = 0, 1, 2,...

min: a sinj = ± 2k (l/2)

k = 1, 2, 3,...

Будуть також спостерігатися побічно max i min у ямах.

4. Явище дифракції на просторовій решітці спостерігається тільки на тілах, розміри яких близькі до довжини хвилі l. Приклад цього – дифракція рентгенівських променів на кристаличній решітці твердого тіла за рахунок того, що період кристалічної решітки d ~ 10^-10 м, l = 10^-10 м, d ~ l.

~ ~

D = AB + BC

AB = BC = d ^. sinJ

D = 2dsinJ,

де d – період решітки кристалу,

J – кут між падаючим променем і площиною кристалу.

d

A C

B

У відбитих променях максимуми інтенсивності спостерігаються за такої умови:

2d sinJ = ml – формула Вульфа–Брегів

m = 1, 2, 3... – порядок дифракційного максимуму.

Дата добавления: 2014-01-07